首页 > 基础资料 博客日记
分布式系统中的那些一致性(CAP、BASE、2PC、3PC、Paxos、ZAB、Raft)
2023-07-24 15:40:43基础资料围观691次
本文介绍 CAP、BASE理论的正确理解、Paxos 算法如何保证一致性及死循环问题、ZAB 协议中原子广播及崩溃恢复以及 Raft 算法的动态演示。
下面还有投票,一起参与进来吧👍
前言
工作过几年的同学,尤其是这几年,大家或多或少都参与过分布式系统的开发,遇到过各式各样“分布式”问题,而遇到这些问题去解决时就是我们对这个知识学习的过程。
不知道大家是否跟我一样,每每搜索到“分布式”关键词,总会出现各种“分布式理论”,比如CAP、BASE理论、2PC、3PC 以及 Paxos、Raft、ZAB 算法,而这些貌似跟一致性都有一定的关系。
在读过数次与之相关的不同文章后,每次都会有不一样的理解以及困惑,比如,CAP中的 C 怎么就强一致了?BASE 理论的定义怎么这么抽象?还有 Paxos、ZAB、Raft 都是一致性算法,奥… 干!!!管求它。转眼就又忘了,不晓得大家是否跟我一样😄。
本文以我对这些一致性理论的理解进行阐述,希望可以对大家有一点帮助。
CAP理论
CAP理论是Eric Brewer教授在2000年提出的,大概是这样的:
在分布式系统中,数据一致性,分区容忍性,系统可用性是不可能同时达到的,只能保证其中两项可以达到。而由于在互联网交互应用中,网络不稳定的情况总是存在,网络分区始终是不可避免的,从而在设计分布式系统时,总是考虑如何在数据一致性和系统可用性上进行取舍。
理解误导
通常在一些CAP的文章中可以看到很多类似以下的说法:
C(consistency)一致性:访问所有节点得到的结果是一致的。
A(Availability)可用性:请求在一定时间内可以得到正确的响应。
P(Partition tolerance)分区容错性:在网络分区的情况下,系统仍能提供服务。
并且后面会跟上这句话分布式系统不能保证同时使用C、A和P,只能选择CP或AP 。
这样的说法并没有错,因为提出该理论的作者确实有提出:
Any distributed system cannot guarantly C,A,and P simultaneously
但是会误导读者去理解。比如在我之前看到上述说法时会有几个疑问:
- 对于分区容错性,我搞个集群就可以;对于一致性,我理解那就跟ACID中的C是不一样的,更像是某个组件集群部署后节点之间的数据一致性,那应该还是集群,为什么说是分布式系统呢?
- 怎么不能保证同时使用C,A, P?怎么一致就不可用了?可用就不一致了?不冲突吧?
CAP是CAP,这个“CP”或“AP”先适当存疑😁

正确的理解
后面去了解CAP理论的背景,得知作者写了2版来阐述CAP,最后一个版本中写道:
In a distributed system(a collection of interconnected nodes that share data),you can only have two out of the following three guarantees across a write/read pair: Consistency,Availability,and Partition Tolerance
在分布式系统(共享数据的互连节点的集合)中,在写/读对中只能有以下三种保证中的两种:一致性、可用性和分区容错
在这一个版本中的(共享数据的互连节点的集合)证实了我第一个疑问,至于为什么说分布式系统,我觉得应该是集群属于分布式系统中的一个场景。
至于第二个疑问其实还是场景问题,如果在没有网络分区的情况下,C,A是可以同时满足的,如果出现了网络分区,C,A确实不可以同时满足,举个例子:如果来了一个写操作,如果要满足一致性,意味着这几个节点的数据要一致后,数据才能被访问,但是出现了网络分区,就会等待网络恢复或重试或者其他操作,必然满足不了可用性的要求(在一定时间内可以得到正确的响应)。反过来,如果要在一定时间内得到正确响应,在网络分区的情况下,一致性必然也满足不了了。
所以CAP理论是有前提和场景的,总结一下应该是这样的:分布式系统中存在共享数据的互连节点,在网络分区的前提下,不能保证同时保证可用性和一致性。
CAP理论的应用
现在再说 Zookeeper 是 CP 架构、Eureka 是 AP 架构 应该就不难理解了。
这两个组件都符合 CAP 中的(共享数据的互连节点的集合),Zookeeper 集群是 Leader 在写数据时需要过半节点同意才会写入,客户端才会读取到这个值,所以说 Zookeeper 是 CP 架构;Eureka 集群是不论哪个节点在写数据时都会立即刷新本地数据然后再同步给其他节点,客户端这个时候读取不同节点时就会发现数据不一致,所以 Eureka 是 AP 架构。
BASE理论
BASE是Basically Available(基本可用)、Soft state(软状态)和 Eventually consistent(最终一致性)三个短语的缩写。
- 基本可用
基本可用是指分布式系统在出现不可预知故障的时候,允许损失部分可用性,不像 CAP 中的定义那样严格(在一定时间内可以得到正确的响应)。比如:- 响应时间上的损失。正常情况下,0.5秒之内返回给用户结果,但由于出现故障,会有重试等操作,3秒内返回也是接受的。
- 系统功能上的损失:正常情况下,用户可以顺利完成每一笔订单,但是在一些节日大促购物高峰的时候,为了保护系统的稳定性,部分用户可能会被引导到一个降级页面。
- 软状态
软状态指允许系统中的数据存在中间状态,这种中间状态的存在不会影响系统的整体可用性。比如:在交易的场景中,因为会存在交易失败的情况,所以不会直接扣减 A 账户100到 B 账户上,而是先冻结 A 账户100。 - 最终一致性
最终一致性是指在经过一段时间后,软状态的数据达到一致的状态。比如:在冻结 A 账户100后,如果失败那就扣减A账户冻结的100至可用余额中;交易成功再将 A 账户冻结的100扣减,并添加至 B 账户的可用余额。最终达到一致性。
有很多的文章说是BASE理论是CAP理论的演进,这种说法先存疑,先存疑😄。因为CAP理论的场景是分布式系统(共享数据的互连节点的集合),而BASE理论是满足更多的场景的。
Paxos算法
Paxos算法是莱斯利·兰伯特于1990年提出的一种基于消息传递且具有高度容错特性的一致性算法。
基于消息传递通信模型的分布式系统,不可避免的会发生以下错误:进程可能会慢、被杀死或者重启,消息可能会延迟、丢失、重复。Paxos 算法解决的问题是在一个可能发生上述异常的分布式系统中如何就某个值达成一致,保证不论发生以上任何异常,都不会破坏决议的一致性。
如何保证一致性?
OK,通过下图看看 Paxos 是如何保证一致性的。为了方便理解,图中的议员暂且当作一个注册中心集群中的实例。
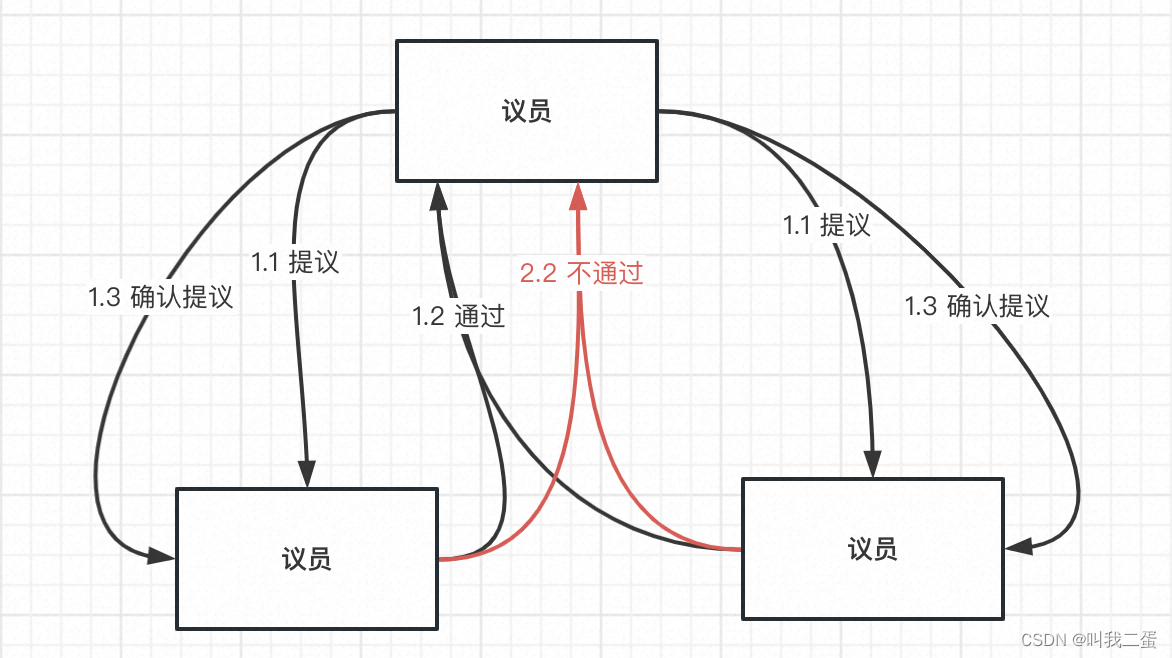
- 当某个议员有某些想法时想让其他议员认可并批准,那么会以提案的方式进行决定。
- 在提交一个提案时都会获取到一个具有全局唯一性的、递增的提案编号(N),然后发送给其他议员。
- 其他议员在收到这个编号后会与自己批准过的提案中最大编号进行比较:
- 如果没有收到的编号(N)大,那么它就会将它已经批准过编号最大的提案响应给提案者,意味着认可这个提案。
- 如果比收到的编号(N)大,则代表编号(N)被处理过,不做任何响应,意味着不认可这个提案。
- 提案者在收到半数以上响应后,就会再次发送一个确认的请求给其它议员进行执行。
- 其他议员在收到确认的请求后,发现没有对编号大于N的提案请求做出过响应,它就批准该提案。
这个我感觉是和2PC一样,通过两阶段提交,最终确认是否批准,只不过是实现细节以及使用场景不同罢了。当然也会存在2PC中第二阶段节点失去通信问题,这种情况议员们最多不批准提案,不会影响一致性问题。
死循环问题
Paxos 算法有几率出现死循环问题,导致提案不通过。如下图:
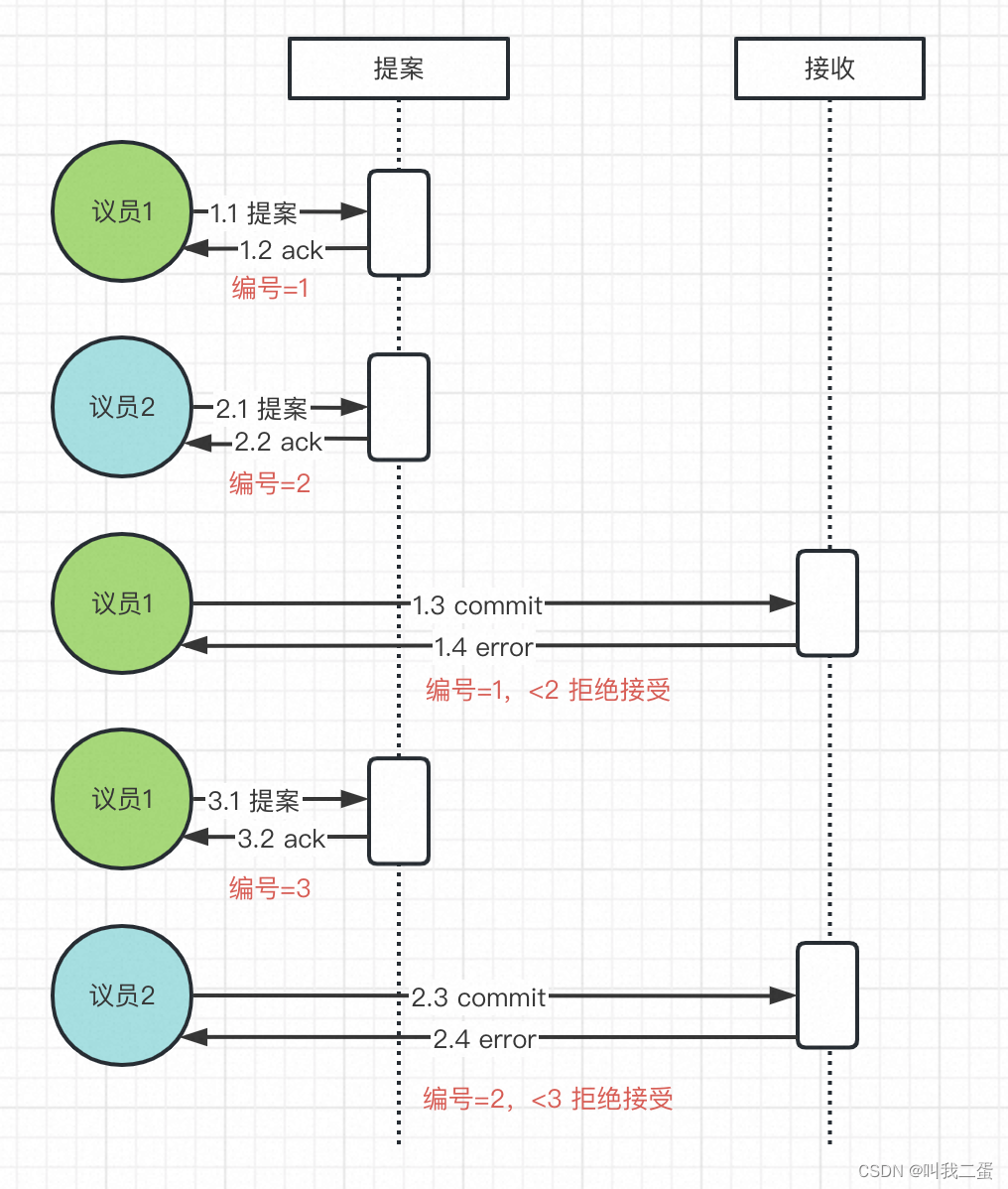
假设我们有2个议员同时发出提案请求。
- 议员1提交编号为1的提案并收到过半响应。
- 此时议员2提交编号为2的提案也收到过半响应。
- 由于提案阶段响应的编号已为2,根据“没有对编号大于N的提案请求做出过响应,它就批准该提案”,所以议员1的编号(1)在接收阶段不会被批准。
- 如果此时议员1重新发送编号为3的提案并通过后,议员2的提案在接收阶段也不会通过。
如此循环,就会造成死循环。
ZAB协议
ZAB 协议(ZooKeeper Atomic Broadcast)原子广播是 ZooKeeper 用来保持所有服务器消息的顺序同步并保证一致,与 Paxos 不同,其为主备架构,所以在同步数据时不会出现多个节点同时提交提案(死循环问题),而是会在集群节点中选举 Leader ** 节点,统一经由 Leader 节点进行提案,但是主备架构避免不了 Leader 节点的崩溃,如果出现该问题,ZAB 还会保证集群节点的崩溃恢复**。关于ZAB更多描述去ZooKeeper官网看看。
所以 ZAB 协议主要做了3件事:
- 选举 Leader 节点。
- 以广播的方式保证副本之间的消息一致。
- Leader 节点崩溃后进行崩溃恢复。
Leader 选举
在这之前先了解下 ZAB 节点的三种状态:
- FOLLOWING:当前节点是跟随者,服从 leader 节点的命令。
- LEADING:当前节点是 leader,负责协调事务。
- LOOKING:节点处于选举状态。
当集群初始启动时,每个节点会投自己一票并向其他节点发起投票请求,进入 LOOKING 状态。当某个节点的投票数过半后,该节点进入LEADING 状态,当选 Leader,其他节点则会进入 FOLLOWING 状态,成为 Follower。下面以3台服务器为例,介绍 Leader 选举过程:
发起投票
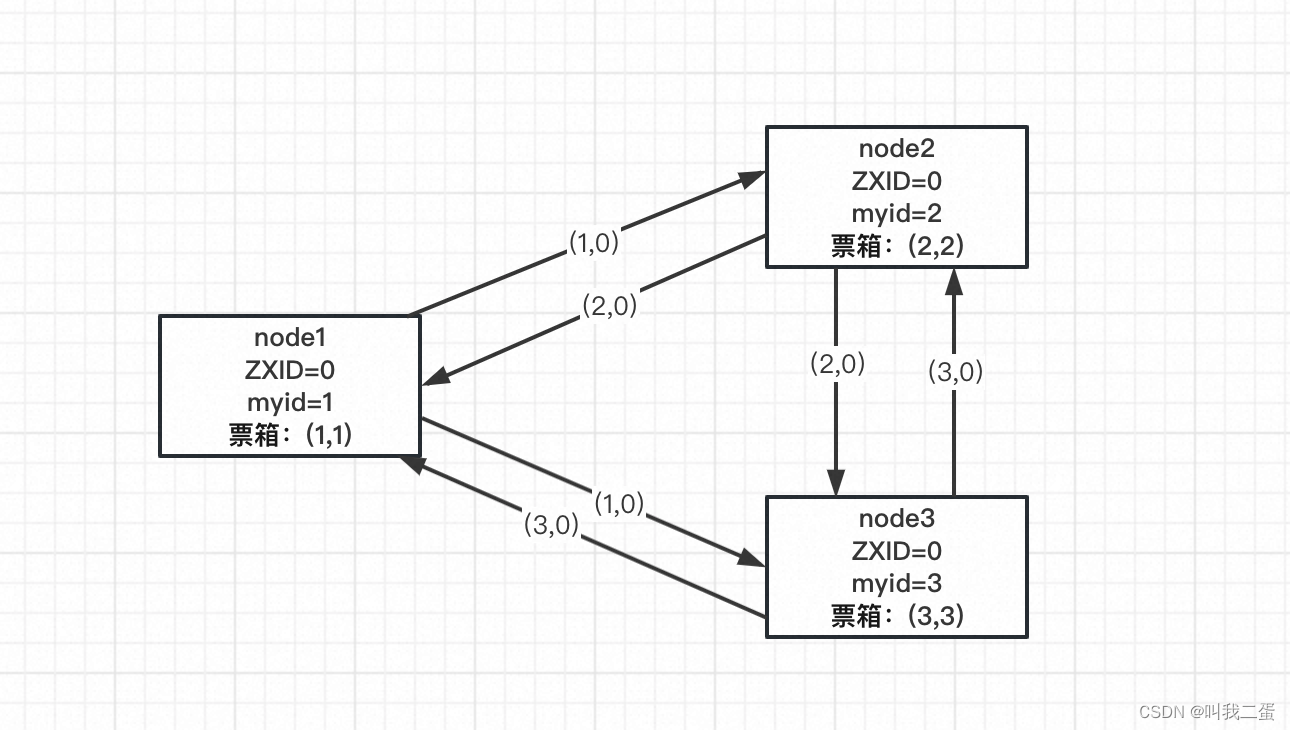
如上图,三个节点同时启动首先会向自己投一票,并将(myid,ZXID)作为投票信息向其他两个节点发送。此时每个节点的投票箱都是自己投个自己(myid,myid)。myid是每个节点的标识;ZXID 是最近一次的事务ID,初始值为0。
PK阶段
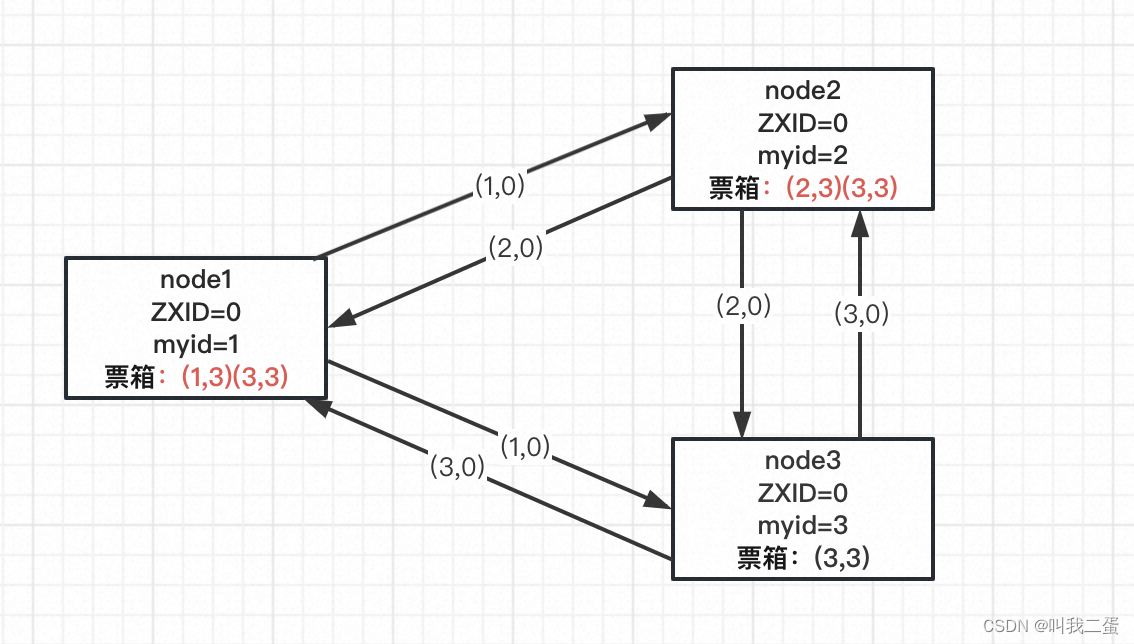
每个节点在收到投票请求后会比较 ZXID,如果 ZXID 相等则比较 myid 。比较时如果自己节点的ZXID或myid小,那么更新自己的投票(myid,胜出节点id)并添加收到的投票至票箱(胜出节点id,胜出节点id)。
如上图,node1 在收到 node2、3 的投票请求后,由于ZXID相等,node3的myid大,所以 node1 更新自己的投票箱并添加 node3 的投票,此时为(1,3)(3,3)。
node2同样如此,投票结果为此时为(2,3)(3,3)。
node3不做更新操作。
广播投票
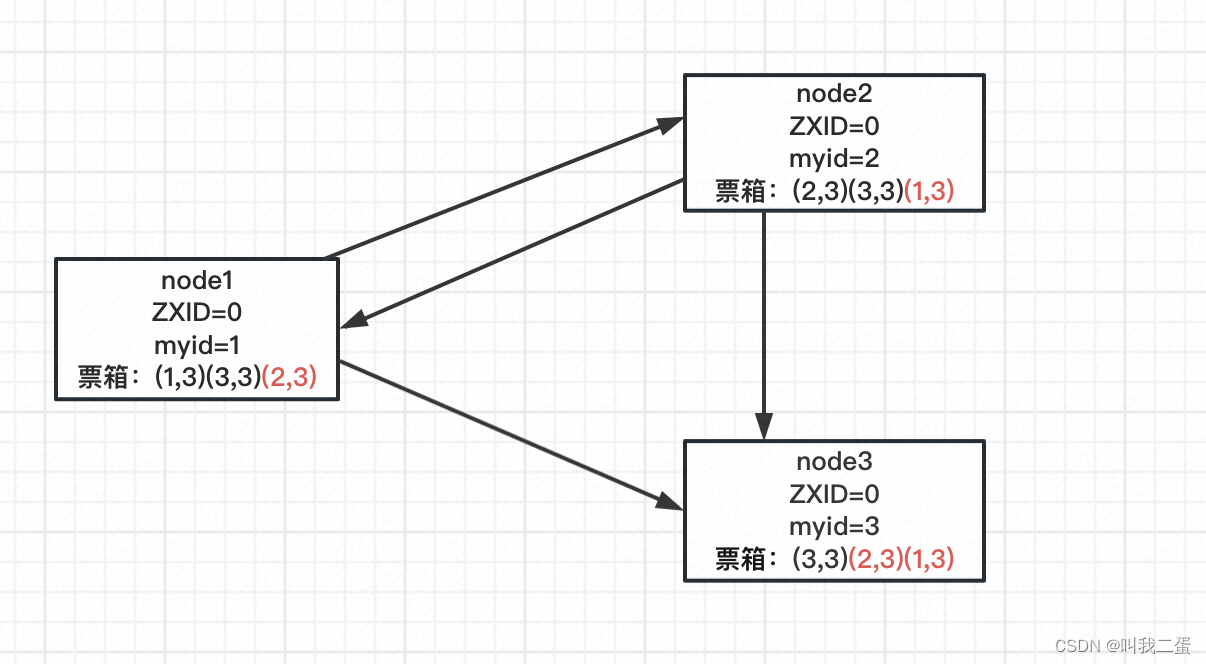
node1、node2 在更新自己的投票结果后向其他两个节点广播投票结果,结果如上图。
根据上述投票,三个服务器一致认为 node3 应该是 Leader 。所以 node3 进入 LEADING 状态成为 Leader,node1、node2 进入 FOLLOWING 状态称为 follower。
下图是搭建了 Zookeeper 集群启动后的结果,也验证上述选举算法。
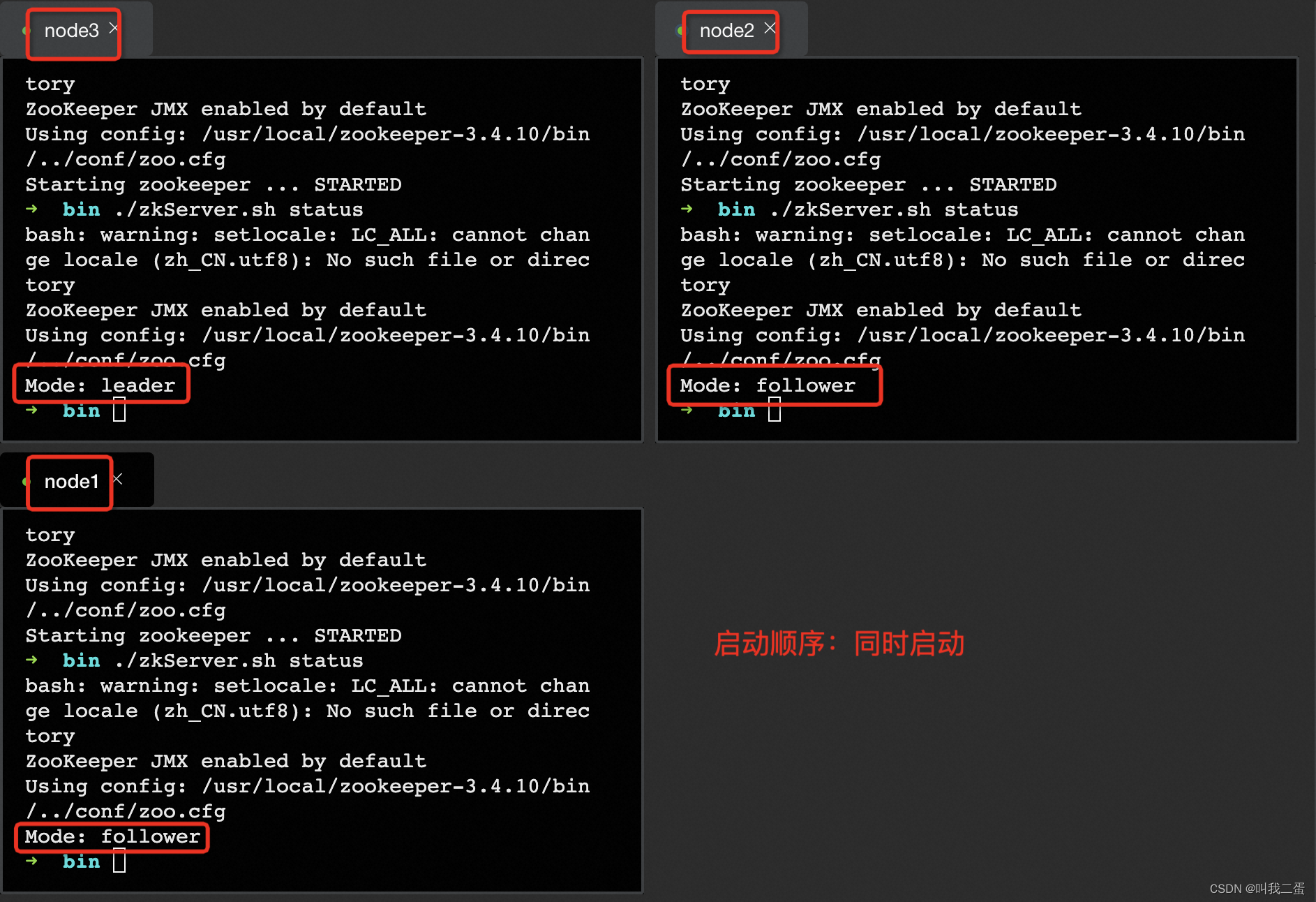
广播消息
为了保障副本之间的数据一致,ZAB协议做了以下几点:
- 所有的写请求都通过 Leader 进行操作,如果 Follower 收到写请求,会转发给 Leader。
- Leader 针对写请求会生成一个提案,并为这个提案生成一个ZXID(保障一致、顺序。)
- Followers 在收到提案后 ack 给 Leader。
- Leader 在收到过半的 Follower ack 后会广播一个 commit 消息。
- Follower 收到 commit 消息后会比较 ZXID,如果之前没有处理过比 ZXID 大的写请求,那就进行提交。
崩溃恢复
Leader 重新选举
当网络异常造成网络分区或者某个节点崩溃,如果是 Leader 节点这时候需要进行重新选举。如下图
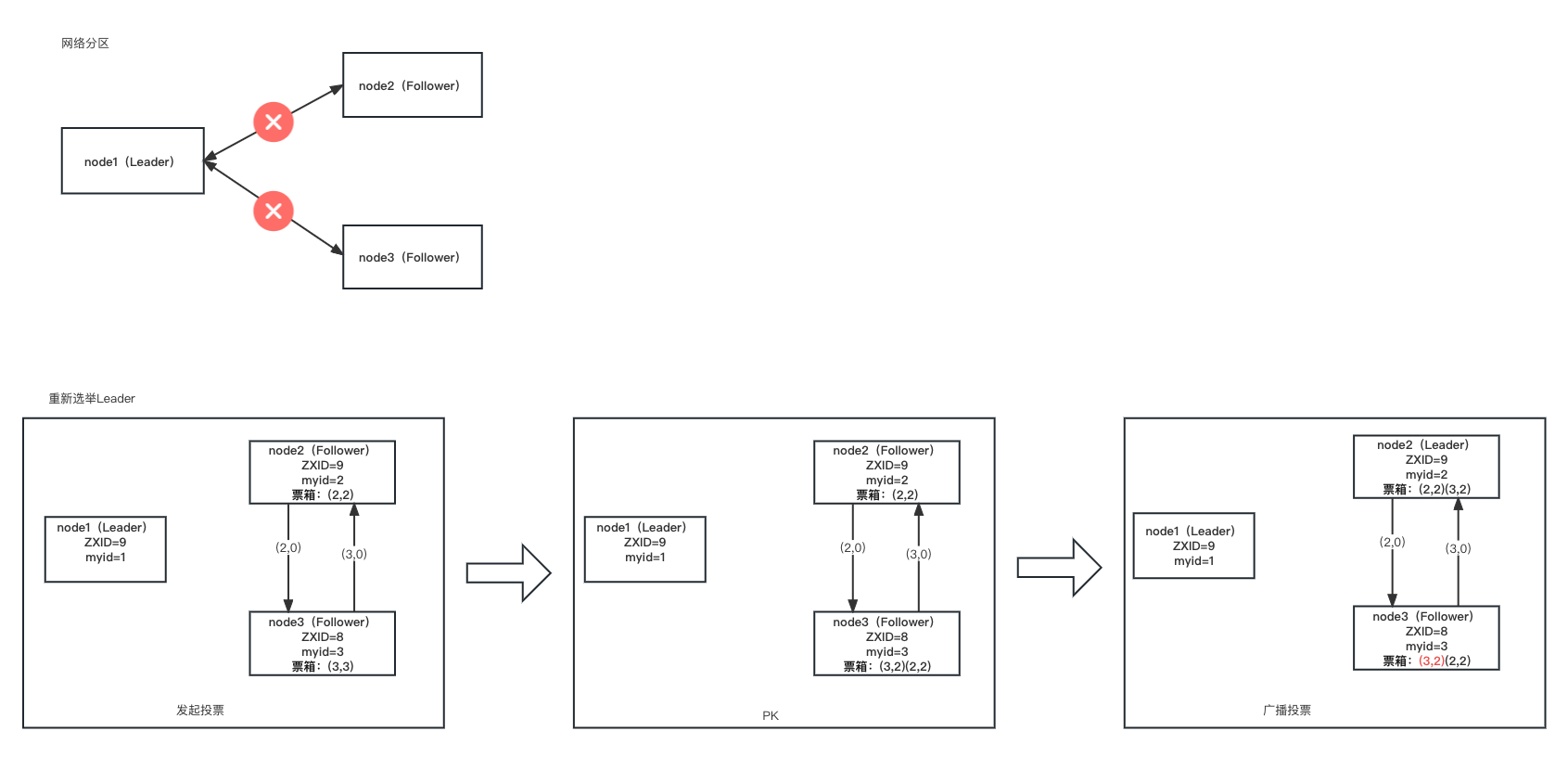
数据同步
选举新的 Leader 后,其他节点的数据要与之同步。同步过程如下图
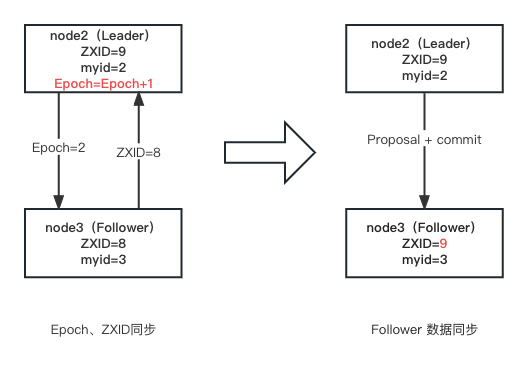
- 在选举为 Leader 后,node2 将自身的 Epoch 进行自增并发送给 Follower,Follower进行更新并将自己的ZXID同步给 Leader 。
每次选举 Leader 后 Epoch 会+1,这样,当老的 Leader 重新连接到集群后,会对比其日志中 epoch 编号与 leader 此时的 epoch 编号:对于 epoch 更小的那部分日志,就舍弃掉。 - Leader 根据 ZXID 的差异进行同步。上图 Leader 会将 Follower 未提交的事务以提案进行逐条发送和提交给 Follower ,Follower 收到提案和提交请求后进行同步。
老 Leader 恢复
当老的 Leader 恢复后要加入集群中,其过程如下:

- node1 发起投票,node2、node3 响应自己的角色和投票,通过 node2 的响应,可以知道 node2 为 Leader ,并且通过两者的投票可以确定 node2 为 Leader ,因此自己成为 Follower。
- 在选举为 Leader 后 将自身的 Epoch 进行自增并发送给 Follower,Follower进行更新并将自己的ZXID同步给 Leader。
- Leader 根据 ZXID 的差异进行同步。上图 ZXID无差异,所以无需同步。
Raft算法
Raft 算法按照我的理解是和ZAB协议相似,两者相同的概念可能名词不同,比如:ZAB 中的 Epoch 和 Raft 的 Term 概念相同;实现方式大体相似,细节不同,比如:数据同步都是通过 Leader 节点进行提案,不同的是 Raft 通过状态达到一致、Leader 选举方式相似,发起投票时都会投自己一票,实现上 Raft 通过两个 timeout 控制选举。这里我就不多废话了,大家可以通过Raft算法动态演示更容易理解。
总结
所以为什么有这么多的一致性定义呢?之间有什么关系?
我觉得还是场景,首先ACID、CAP、BASE都是理论,ACID是专注于事务、CAP理论作用在集群副本场景、BASE理论应用最终一致性场景。
而2PC、3PC则是对于事务完整性的具体解决方案,Paxos、ZAB、Raft更倾向于集群副本一致性的解决方案。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若内容造成侵权/违法违规/事实不符,请联系邮箱:jacktools123@163.com进行投诉反馈,一经查实,立即删除!
标签:

