【数据结构】第十六弹---C语言实现希尔排序

文章【数据结构】第十六弹---C语言实现希尔排序分享给大家，欢迎收藏Java资料网，专注分享技术知识

✨个人主页： 熬夜学编程的小林

💗系列专栏： 【C语言详解】 【数据结构详解】【C++详解】

目录

1、希尔排序( 缩小增量排序 )

1.1、预排序实现

1.2、希尔排序代码实现

1.3、代码测试

1.4、时空复杂度分析

1.5、性能比较

总结

---

上一弹我们学习了直接插入排序，通过时空复杂度分析，时间复杂度为O(N^2)，一般情况效率较低，有没有对直接插入排序进行优化的排序呢？？？没错，我们这一弹讲解的排序就是对直接插入排序的优化的排序！！！
 

1、希尔排序( 缩小增量排序 )

希尔排序是一种基于插入排序的算法，通过引入增量的概念来改进插入排序的性能

希尔排序法又称缩小增量法。希尔排序法的基本思想是：将原始列表分成多个子列表，先对每个子列表进行插入排序，然后逐渐减少子列表的数量，使整个列表趋向于部分有序，最后当整个列表作为一个子列表进行插入排序时，由于已经部分有序，所以排序效率高。这个过程中，每次排序的子列表是通过选择不同的“增量”来确定的。

动图如下： 

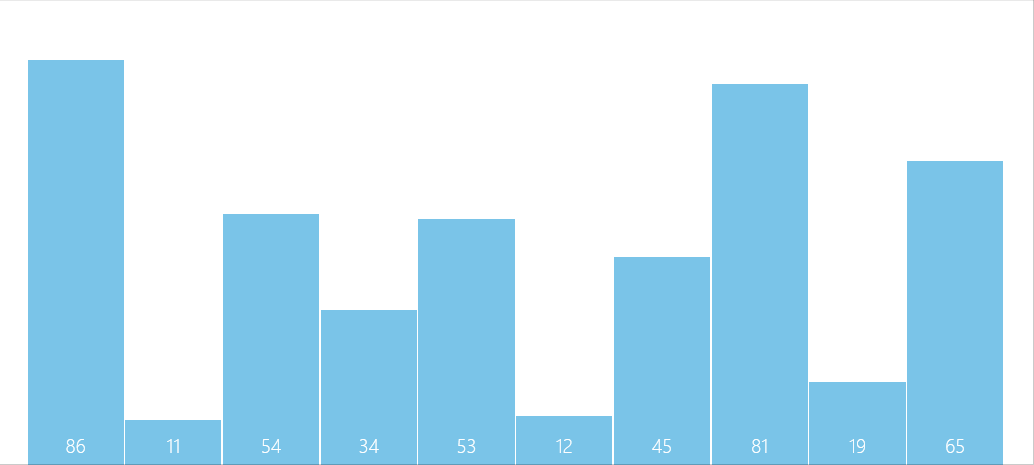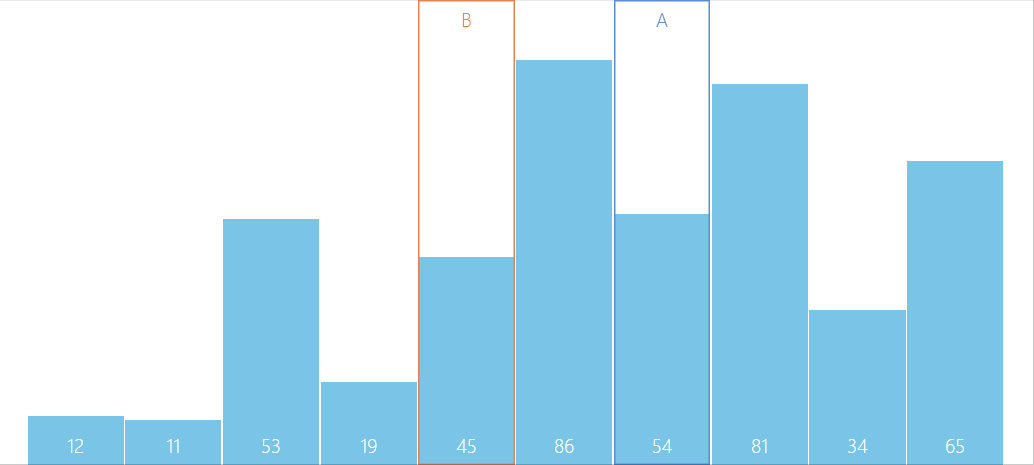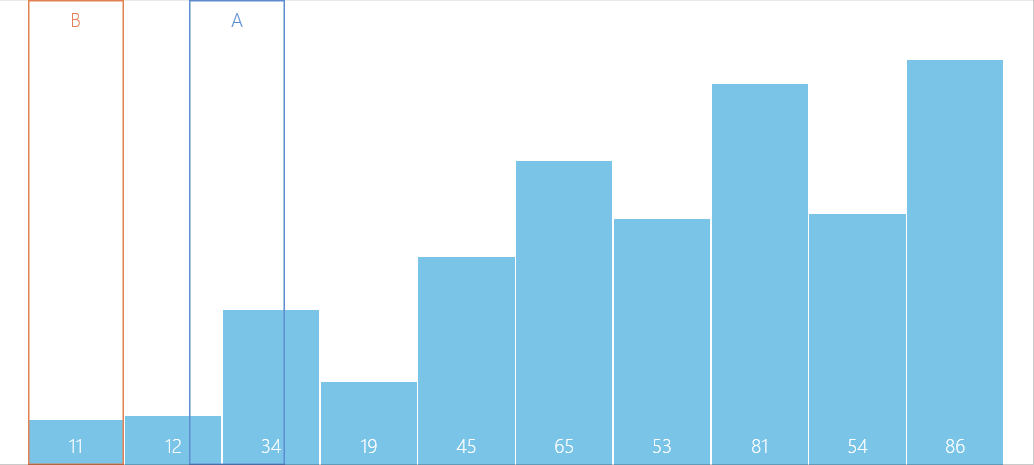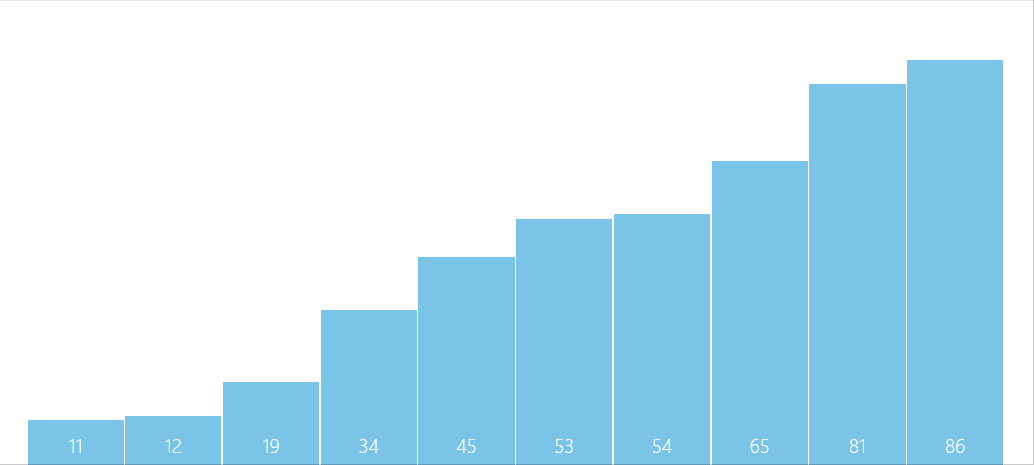
实现思路

1. 预排序
2. 直接插入排序

1.1、预排序实现

预排序：

根据当前增量，数组被分为若干子序列，这些子序列的元素在原数组中间隔着固定的增量。对每个子序列应用插入排序。

假设当前增量为5：

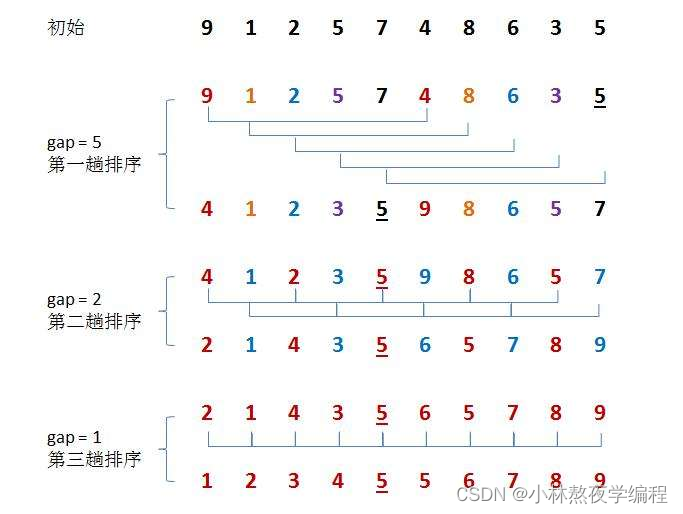
首先，增量为5，我们将数组元素分为增量（5）个子序列，每个子序列由原数组中相隔增量位置上的元素组成。所以我们有如下子序列：

子序列1: 9，4
子序列2: 1，8
子序列3: 2，6

子序列4: 5，3
子序列5: 7，5

然后对每个子序列进行独立的插入排序：

子序列1排序后：4，9
子序列2排序后：1，8
子序列3排序后：2，6

子序列2排序后：3，5
子序列3排序后：5，7

一趟排序之后的数组：

4 1 2 3 5 9 8 6 5 7

完成了一轮希尔排序，此时整个数组并不完全有序，但是已经比原始的数组更接近有序了。然后减小增量，通常是将原来的增量除以2（或者除以3+1），现在选择下一个增量为 2，按照此排序规则继续预排序即可，直到增量为1时，则为直接插入排序，此时则排序完成。

一个子序列排序实现：

int gap;
int end;
int tmp = a[end + gap];
while (end >= 0)
{
	if (a[end] > tmp)
	{
		a[end + gap] = a[end];
		end-=gap;
	}
	else
    {
		break;
    }
}
a[end + gap] = tmp;

与直接插入代码不同的是，这里对end所加减的均为gap；

单次插入完成后，我们来控制单个子序列的整个过程，每实现一次排序，下一次插入的数据为end+gap。

单趟排序实现：

int gap;

for (int i = 0; i < n-gap; i += gap)
{
	int end = i;
	int tmp = a[end + gap];
	while (end >= 0)
	{
		if (a[end] > tmp)
		{
			a[end + gap] = a[end];
			end -= gap;
		}
		else
        {
			break;
	    }
    }
	a[end + gap] = tmp;
}

这里for循环的条件为 i <n-gap 防止数组越界.

完成单个子序列的排序后，我们再对整个子序列排序：

int gap;
for (int j = 0; j < gap; j++)
{
	for (int i = 0; i < n - gap; i += gap)
	{
		int end = i;
		int tmp = a[end + gap];
		while (end >= 0)
		{
			if (a[end] > tmp)
			{
				a[end + gap] = a[end];
				end -= gap;
			}
			else
            {
				break;
		    }
       }
		a[end + gap] = tmp;
	}
}

外层循环（for (int j = 0; j < gap; j++)）意在对每个以gap为间隔的分组进行遍历。

优化：

这串代码三层循环的逻辑是按照每一组排序完成后再进行下一组排序的，事实上我们可以不需要最外层的循环。

int gap = 3;
	
for (int i = 0; i < n - gap; i++)
{
	int end = i;
	int tmp = a[end + gap];
	while (end >= 0)
	{
		if (a[end] > tmp)
		{
			a[end + gap] = a[end];
			end -= gap;
		}
		else
        {
			break;
	    }
    }
	a[end + gap] = tmp;
}

这里我们将原先代码中的i += gap修改为i++，意味着这次不是按照一组一组进行了，是一次排序完每个组的第二个元素，再进行下一个元素的排序。 

1.2、希尔排序代码实现

我们先对预排序的增量进行分析：

gap越大，大的值更快调到后面，小的值更快调到前面，越不接近有序。
gap越小，大的值更慢调到后面，小的值更慢调到前面，越接近有序。
当gap为1，就是直接插入排序。

所以在实现希尔排序时，给gap固定值是行不通的。

因此，gap的值是应该随着n来变化的，实现多次预排。为了满足gap最终为1，博主推荐的方式是先将gap赋值成n，然后在排序的时候将gap赋值成gap/3+1(或者gap/2)。

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;//博主写的是/3+1也可以是gap/2
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
                {
					break;
                }
			}
			a[end + gap] = tmp;
		}
	}
}

这里无论gap是奇数还是偶数，这里gap最终都会除以到值为1。

在这里：

gap>1时是预排序，目的让其接近有序。
gap=1时是直接插入排序，目的让其有序。
在gap=1时，已经十分接近有序了。

这里gap预排序次数还是有点多，因此我们可以再次进行修改，让gap每次除以3，为了使gap最后能回到1，我们进行加一处理。

 注意：

1. 此处都是每隔gap进行插入。

2. gap不是一定为gap/3 + 1，也可以是gap /2 ，原因是当gap等于1的时候就是直接插入排序，进行一次排序即可变成有序，所以只要最后的gap为1都是可以的。 

1.3、代码测试

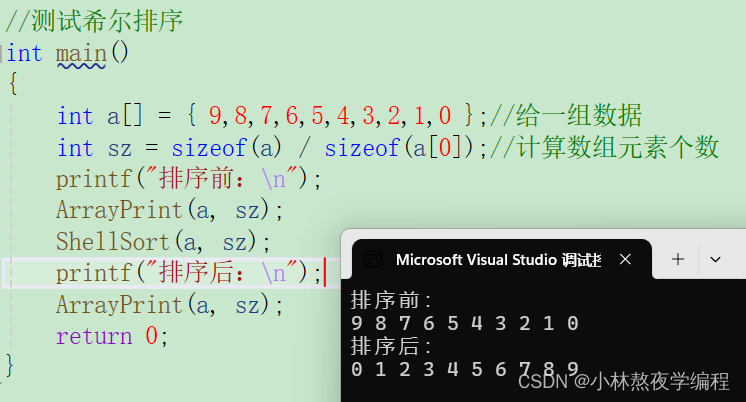
测试代码：

//测试希尔排序
int main()
{
	int a[] = { 9,8,7,6,5,4,3,2,1,0 };//给一组数据
	int sz = sizeof(a) / sizeof(a[0]);//计算数组元素个数
	printf("排序前：\n");
	ArrayPrint(a, sz);
	ShellSort(a, sz);
	printf("排序后：\n");
	ArrayPrint(a, sz);
	return 0;
}

测试结果：

1.4、时空复杂度分析

希尔排序的时间复杂度并不固定，它依赖于所选择的间隔序列（增量序列）。直到今天，已经有多种不同的间隔序列被提出来，每种都有自己的性能特点。

《数据结构(C语言版)》--- 严蔚敏
 

《数据结构-用面相对象方法与C++描述》--- 殷人昆

时间复杂度：

因为咋们的gap是按照Knuth提出的方式取值的，而且Knuth进行了大量的试验统计，我们暂时就按照：O(N^1.25) 到  O(1.6* N^1.25) 来算。

空间复杂度：

插入排序的空间复杂度为O(1)，因为它是一个原地排序算法，不需要额外的存储空间来排序。

1.5、性能比较

我们在前面一弹提到了clock()函数可以获取程序启动到函数调用时之间的CPU时钟周期数，我们在这里通过具体的排序算法来进行比较性能。

注意：clock()函数的头文件是#include<time.h>，时间的单位为毫秒。

性能比较的思想是通过比较两个函数所运行的时间大小。通过clock计算排序前的程序运行的时间，再计算排序结束程序运行的时间，时间的差值则为排序运行的时间。

尽量使用release模式进行测试，因为release效率更高。

测试代码：

void TestOP()
{
	srand(time(0));//随机数种子
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);//动态开辟N个元素
	int* a2 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand() + i;//随机数只有3万，为了更加随机再加上i
		a2[i] = a1[i];
	}
    //clock计算程序运行到此时的时间 毫秒
	int begin1 = clock();//排序前程序运行时间
	InsertSort(a1, N);
	int end1 = clock();//排序后程序运行时间
	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();
	printf("InsertSort:%d\n", end1 - begin1);//程勋运行时间的差值即排序运行的时间
	printf("ShellSort:%d\n", end2 - begin2);
	free(a1);//释放空间
	free(a2);
}

当N为10万时，release版本测试出来的结果： 

 

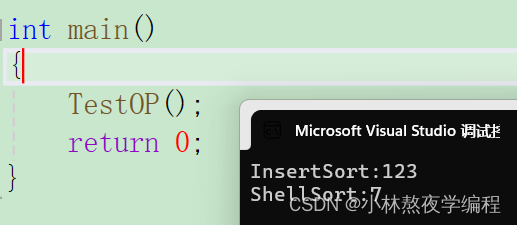
 当N为100万时，release版本测试出来的结果： 

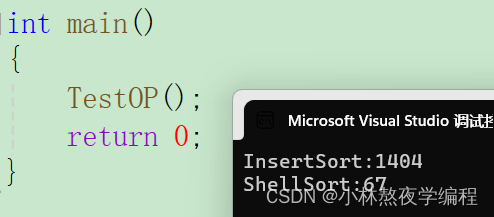
明显能够看到希尔排序的效率比直接插入排序的效率高很多，当N为10万的时候，希尔排序是直接插入排序的18倍，当N为10万的时候，希尔排序是直接插入排序的20倍。

希尔排序的特性总结：

时间复杂度：O(N²)

空间复杂度：O(1)

稳定性：不稳定

复杂性：简单

总结

本篇博客就结束啦，谢谢大家的观看，如果公主少年们有好的建议可以留言喔，谢谢大家啦！

文章来源:https://blog.csdn.net/2201_75584283/article/details/136968423
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！