首页 > 基础资料 博客日记
java中常见数据结构
2024-04-12 09:00:05基础资料围观628次
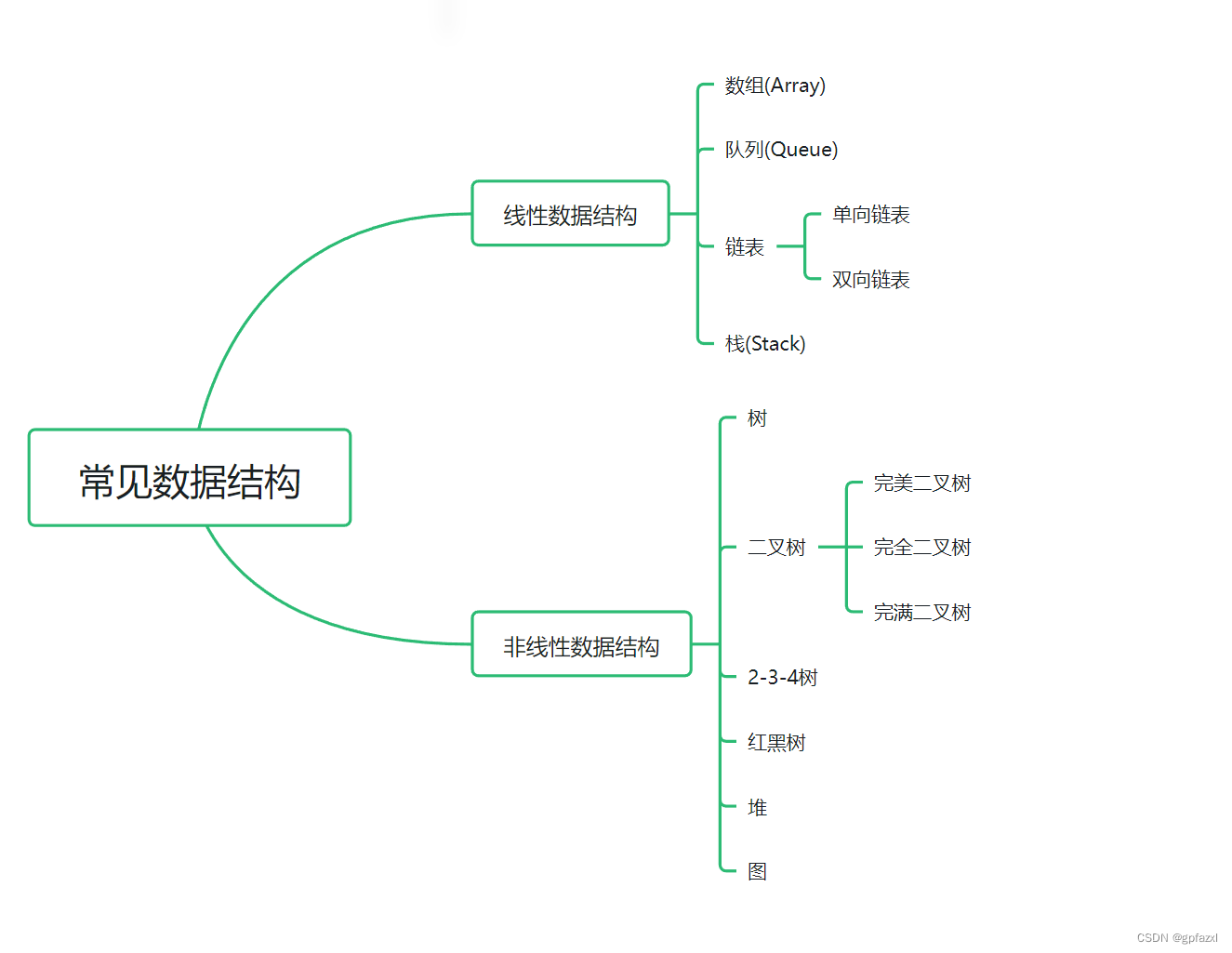
java中常见数据结构
1. 线性数据结构
线性表: 线性表就是数据排成像一条线的结构。每个线性表上的数据最多只有前和后两个方向。
线性表结构:数组、链表、队列、栈
数据结构演示地址: 数据结构可视化
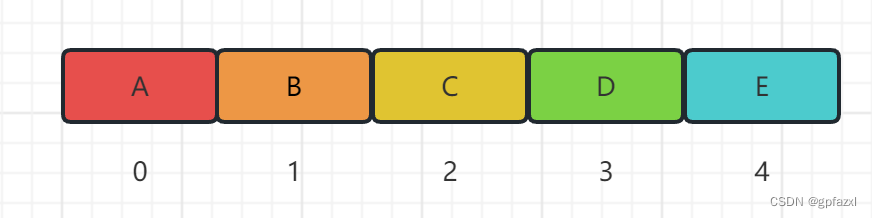
1.1 数组
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一组具有相同类型的数据。
// 动态初始化:初始化时由程序员只指定数组长度,由系统为数组元素分配初始值
char c1[] = new char[5];
// 静态初始化: 初始化时由程序员显示置顶每个数组的初始值,由系统决定数组长度
char c2[] = new char[]{'A','B','C','D','E'};
char c3[] = {'A','B','C','D','E'};
具有如下的特点:
- 内存地址连续
- 检索效率高(可以通过下标访问成员)
- 增删操作效率低(保证数据越界的问题,需动态扩容)
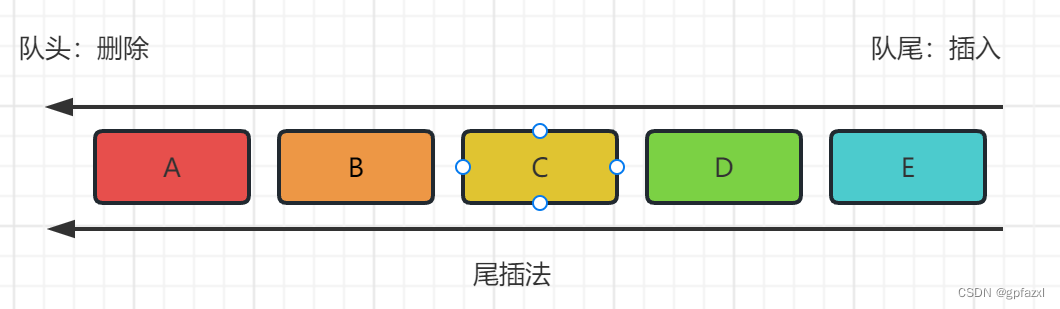
1.2 队列
队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
队列中数据的特点:先进先出,后进后出。
队列的操作:类似一个排队机制。允许插入的一端称为队尾,允许删除的一端称为队头。我们可以将其想象成一个链表,队头就是这个链表中的第一个节点,队尾就是这个链表中的最后一个节点,然而我们只能对这个链表进行 尾插、头删操作。
Java代码测试实现
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);//尾插
queue.offer(2);
queue.offer(3);
queue.offer(4);
System.out.println(queue);
System.out.println(queue.peek());//访问队列头元素
System.out.println(queue);
System.out.println(queue.poll());//删除队列头元素
System.out.println(queue);
}
输出结果:
[1, 2, 3, 4]
1
[1, 2, 3, 4]
1
[2, 3, 4]
1.3 链表
- 链表是线性数据结构
- 内存地址不连续
- 每个节点里存储了下个节点的指针
1.3.1 单向链表
单向链表(单链表)是链表的一种,它由节点组成,每个节点都包含下一个节点的指针,下图就是一个单链表,表头为空,表头的后继节点是"节点10"(数据为10的节点),“节点10"的后继节点是"节点20”(数据为10的节点)

然后我们来看下删除链表的操作,比如删除30这个节点
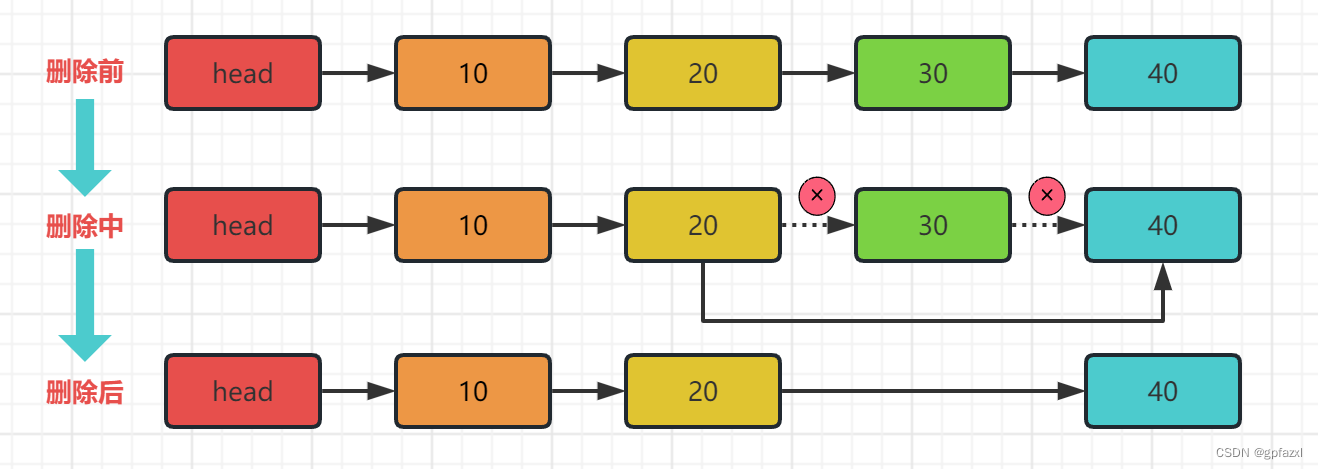
在上面的结构基础上我们再来添加一个节点到链表中
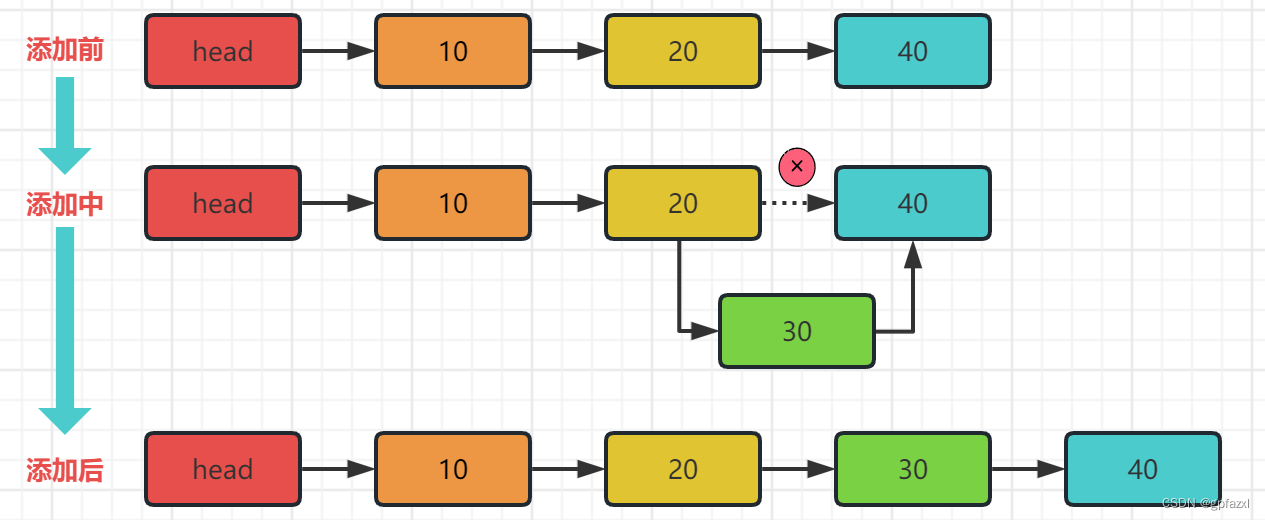
1.3.2 双向链表
双向链表(双链表)是链表的一种。和单链表一样,双链表也是由节点组成,它的每个数据节点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个节点开始,都可以很方便地访问它的前驱节点和后继节点。一般我们都构造双向循环链表。
双链表的示意图如下:

双向链表的具体实现可以参考:
static final class Node {
// 前一个节点
volatile Node prev;
// 后一个节点
volatile Node next;
// 链表节点存储的具体数据
volatile Thread thread;
}
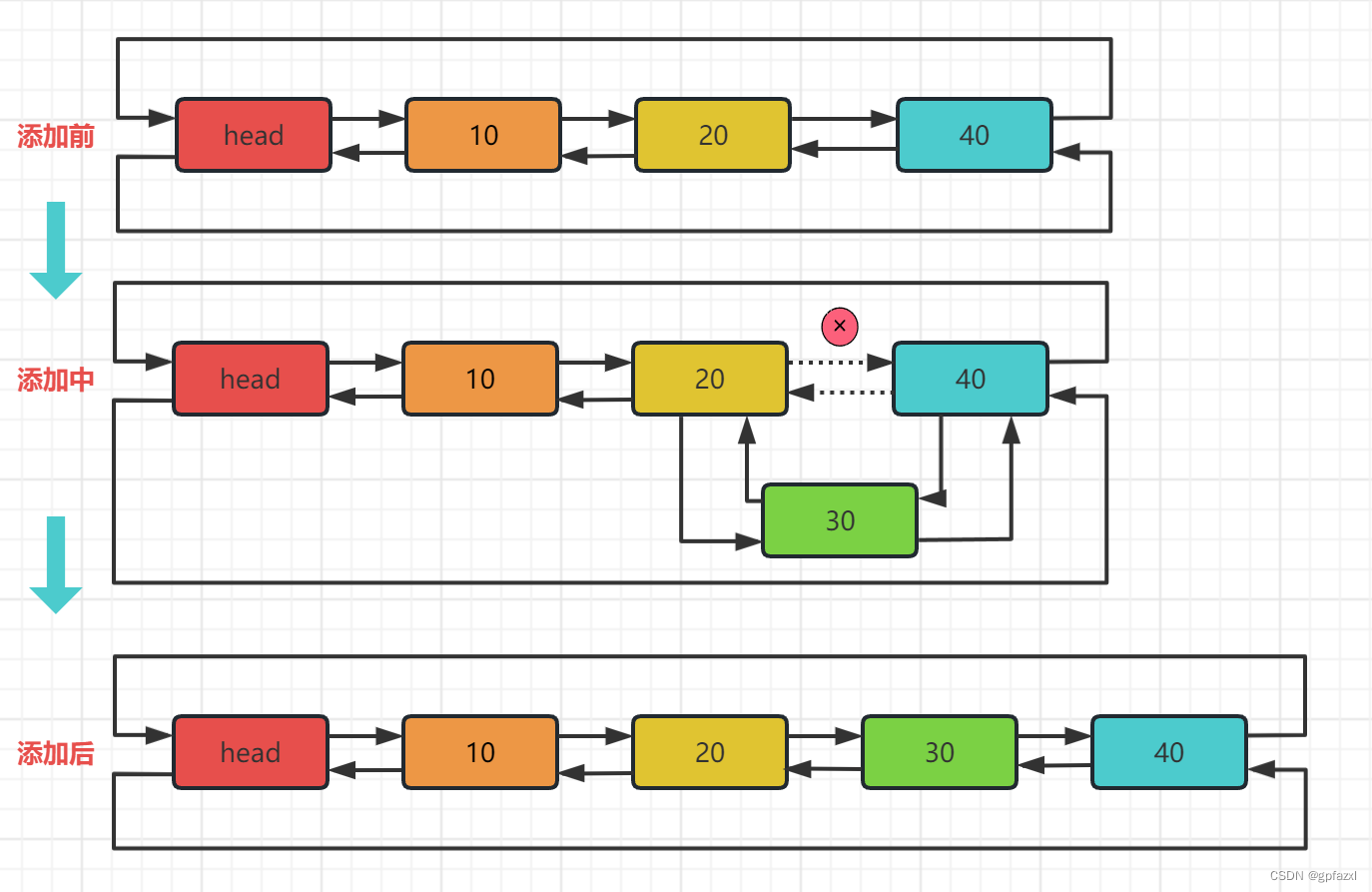
我们看看双向链表删除节点的操作,比如说下面这个单链表中我们要删除"节点30"。
删除之前:“节点20"的后继节点为"节点30”,“节点30” 的前继节点为"节点20"。“节点30"的后继节点为"节点40”,“节点40” 的前继节点为"节点30"。
删除之后:“节点20"的后继节点为"节点40”,“节点40” 的前继节点为"节点20"。
我们再来看看双向链表添加节点的操作,比如说下面这个双向链表在"节点20"与"节点40"之间添加"节点30"
添加之前:“节点20"的后继节点为"节点40”,“节点40” 的前继节点为"节点20"。
添加之后:“节点20"的后继节点为"节点30”,“节点30” 的前继节点为"节点20"。“节点30"的后继节点为"节点40”,“节点40” 的前继节点为"节点30"。
1.4 栈
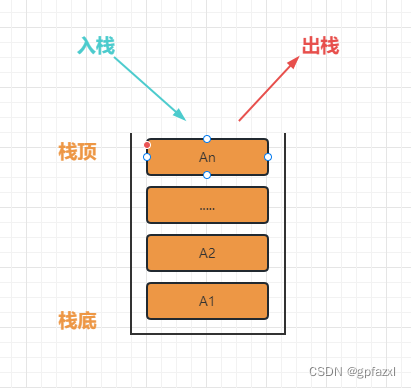
栈(stack)是限定仅在表尾进行插入或者删除的线性表。对于栈来说,表尾端称为栈顶(top),表头端称为栈低(bottom)。不含元素的空表称为空栈。因为栈限定在表尾进行插入或者删除,所以栈又被称为后进先出的线性表(简称LIFO:Last in, First out.结构)。
2. 非线性数据结构
非线性表:与线性表对立,在非线性表之中,数据之间并不是简单的前后关系。
非线性表结构:二叉树、堆、图等。
2.1 树
树[Tree]是n(n>=0)个节点的有限集。n=0时称为空树。在任意一颗非空树中:
- 有且仅有一个特定的称为根[Root]的节点;
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1、T2、…、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
- 根节点是唯一的,不可能存在多个根节点,数据结构中的树只能有一个根节点。
- 子树的个数没有限制,但它们一定是互不相交的。
如图,是一棵普通树
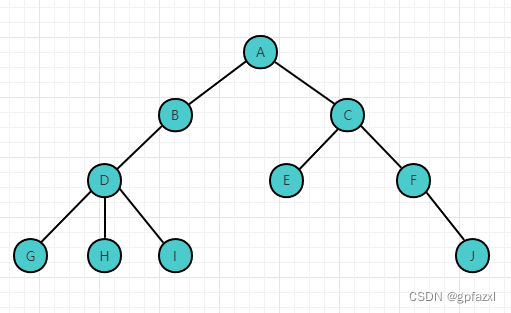
度数:节点拥有的子节点的数目称为节点的 度 。
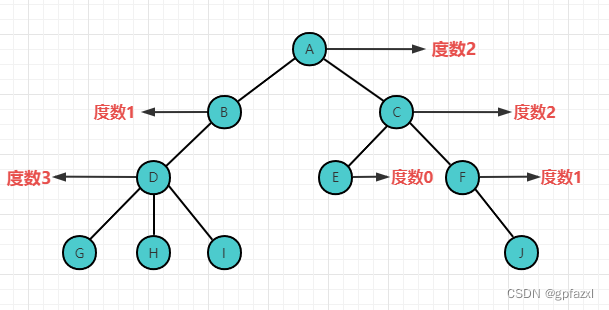
节点关系:
- 孩子节点
- 双亲节点
- 兄弟节点
节点层次:
从根开始定义起,根为第一层,根的孩子为第二层,以此类推。

树的深度:树中节点的最大层次,如上图深度为4
2.2 二叉树
2.2.1 概念介绍
二叉树 :每个节点最多有两个子节点的树就是二叉树(即二叉树中不存在度大于2的节点)。二叉树的子树有左右之分,其次序不能任意颠倒。
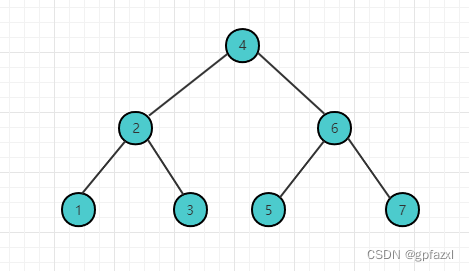
二叉查找树也称为有序二叉查找树,满足二叉查找树的一般性质,是指一棵空树具有如下性质:
- 任意节点左子树不为空,则左子树的值均小于根节点的值
- 任意节点右子树不为空,则右子树的值均大于于根节点的值
- 任意节点的左右子树也分别是二叉查找树
- 没有键值相等的节点
二叉树又分为:
- 完美二叉树
- 完全二叉树
- 完满二叉树
完美二叉树 》》 完全二叉树 》》 完满二叉树
完美二叉树:又称为 满二叉树 ,除了叶子节点之外的每一个节点都有两个孩子节点,每层都被完全填充
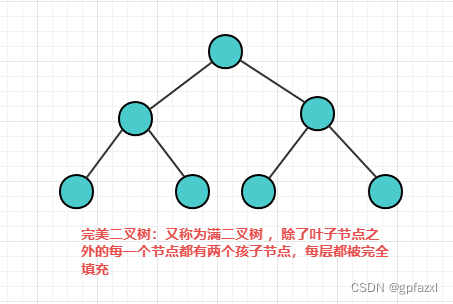
完全二叉树:除了最后一层之外的其他每一层都被完全填充,并且所有的节点都保持向左对齐
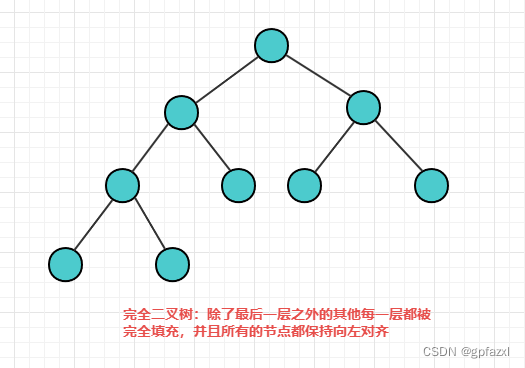
完满二叉树:除了叶子节点之外的每一个节点都有两个孩子节点。

2.2.2 遍历操作
二叉树中的遍历规则有如下三种:
中序遍历:所谓的中序遍历就是先访问左节点,再访问根节点,最后访问右节点,即左-根-右遍历
先序/前序遍历:所谓的前序遍历就是先访问根节点,再访问左节点,最后访问右节点,即根-左-右遍历
后序遍历:所谓的后序遍历就是先访问左节点,再访问右节点,最后访问根节点。即左-右-根遍历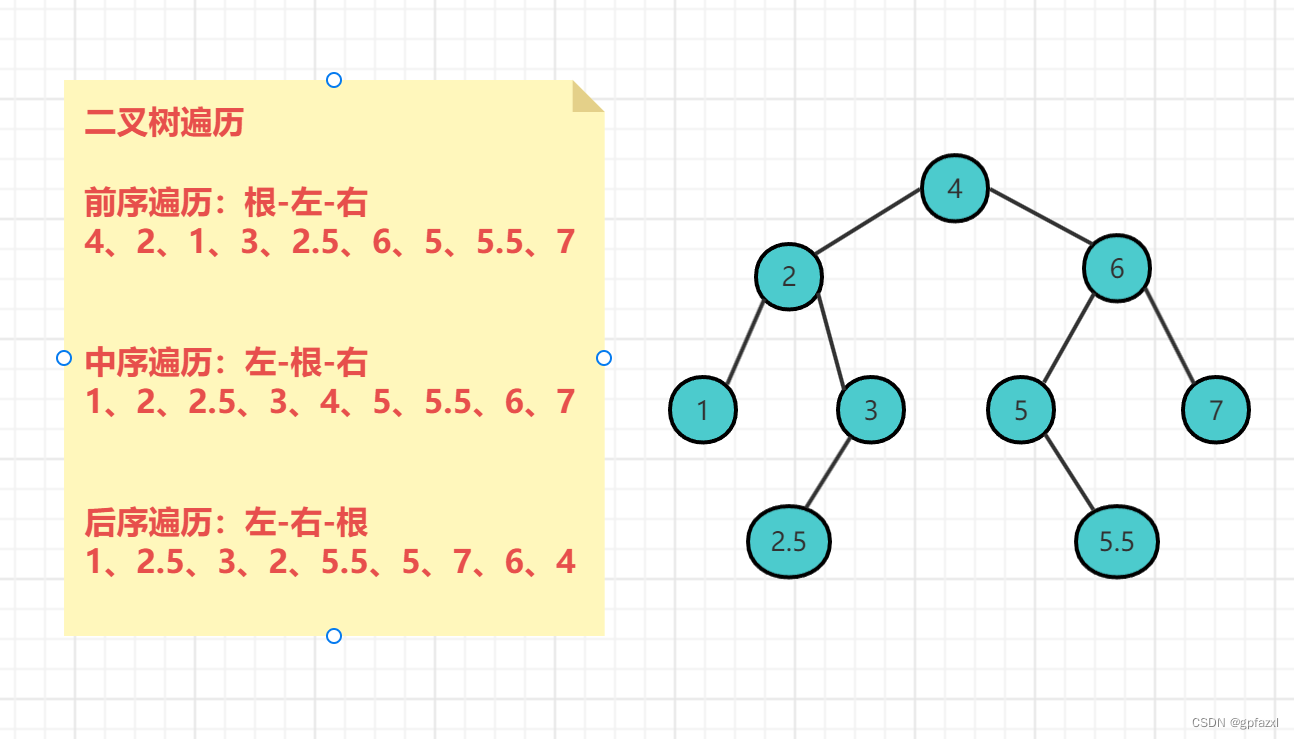
查找最小值:沿着根节点的左子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最小节点
查找最大值:沿着根节点的右子树一路查找,直到最后一个不为空的节点,该节点就是当前这个树的最大节点
查找前驱节点 :小于当前节点的最大值
查找后继节点 :大于当前节点的最小值
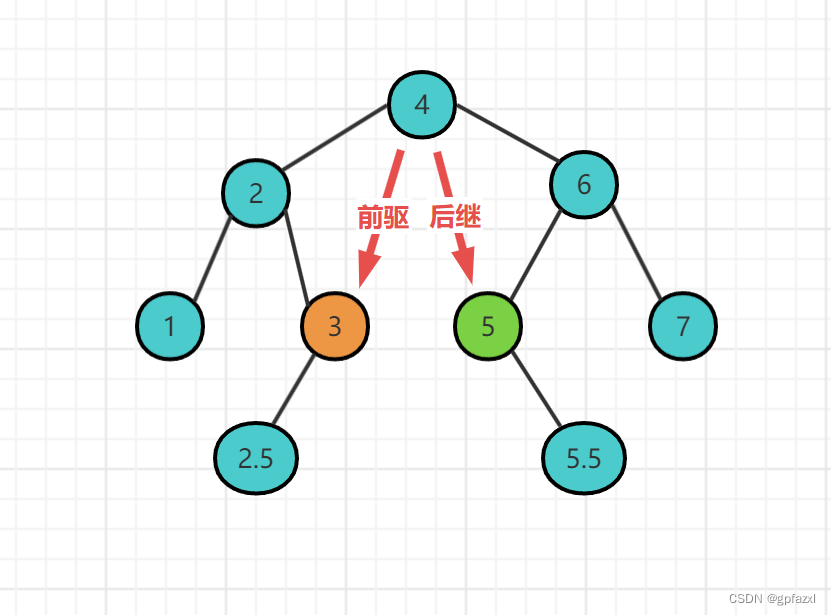
2.2.3 删除节点
二叉树中的删除节点:本质上是找前驱节点或者后继节点来替代
- 叶子节点直接删除
- 只有一个子节点的用子节点替代(本质上就是找的前驱节点或者后继节点,左节点就是前驱节点,右节点就是后继节点)
- 有两个子节点的,需要找到替代节点(替代节点就是前驱节点或者后继节点)
2.2.4 查找局限性
一个二叉查找树是由n个节点随机构成,所以,对于某些情况,二叉查找树会退化成一个有n个节点的线性链.如下图:
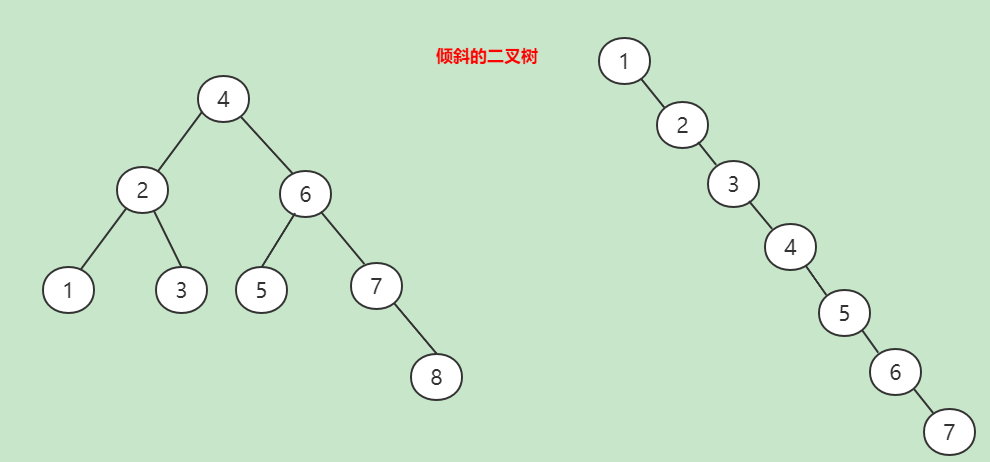
2.2.5 AVL
BST存在的问题是,树在插入的时候会导致倾斜,不同的插入顺序会导致数的高度不一样,而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上,这样树的高度为N。基于BST存在的问题,平衡查找二叉树(Balanced BST)产生了。平衡树的插入和删除的时候,会通过旋转操作将高度保持在LogN。其中两款具有代表性的平衡术分别为AVL树(高度平衡树,具备二叉搜索树的全部特性,而且左右子树高度差不超过1)和红黑树。
AVL树是如何实现平衡的呢?,具体是通过左旋或者右旋来实现的。具体如下图:
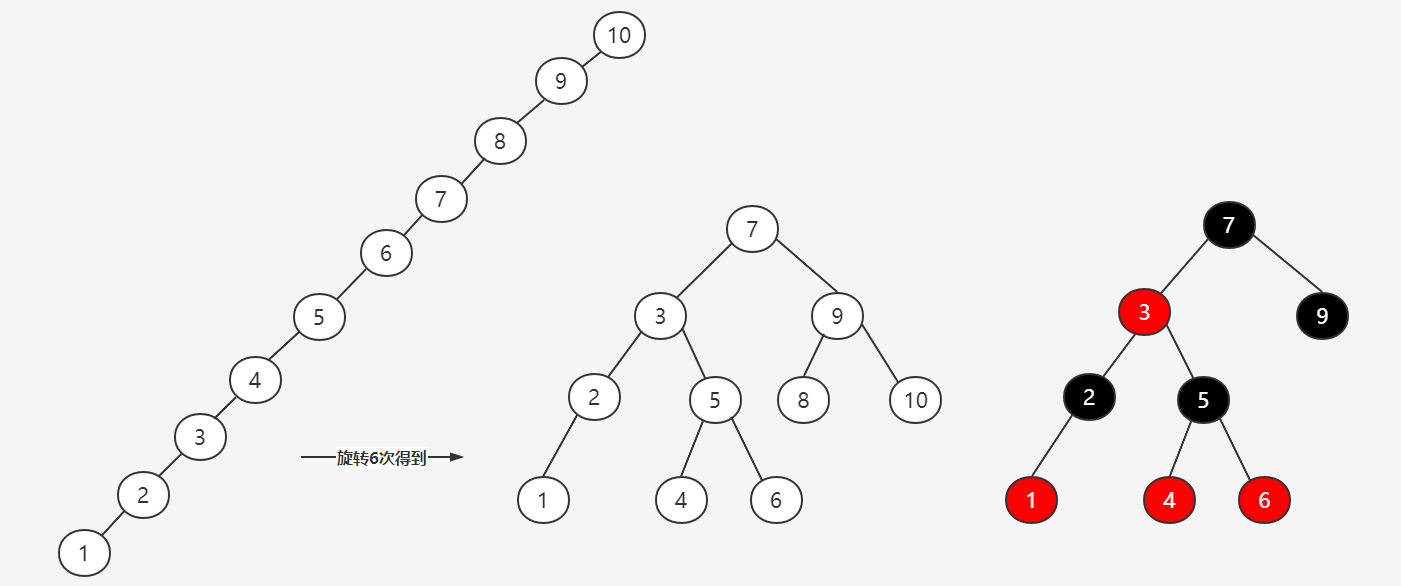
虽然AVL可以解决二叉树所存在的问题,但是AVL树要求太过严格,左旋和右旋的开销会比较大,这时出现了红黑树,只要求黑色节点平衡即可.
2.3 2-3-4树
1 概念介绍
2-3-4树是四阶的 B树(Balance Tree),他属于一种多路查找树,它的结构有以下限制:
所有叶子节点都拥有相同的深度。
节点只能是 2-节点、3-节点、4-节点之一。
- 2-节点:包含 1 个元素的节点,有 2 个子节点;
- 3-节点:包含 2 个元素的节点,有 3 个子节点;
- 4-节点:包含 3 个元素的节点,有 4 个子节点;
所有节点必须至少包含1个元素
元素始终保持排序顺序,整体上保持二叉查找树的性质,即父节点大于左子节点,小于右子节点;
而且节点有多个元素时,每个元素必须大于它左边的和它的左子树中元素。
下图是一个典型的 2-3-4树
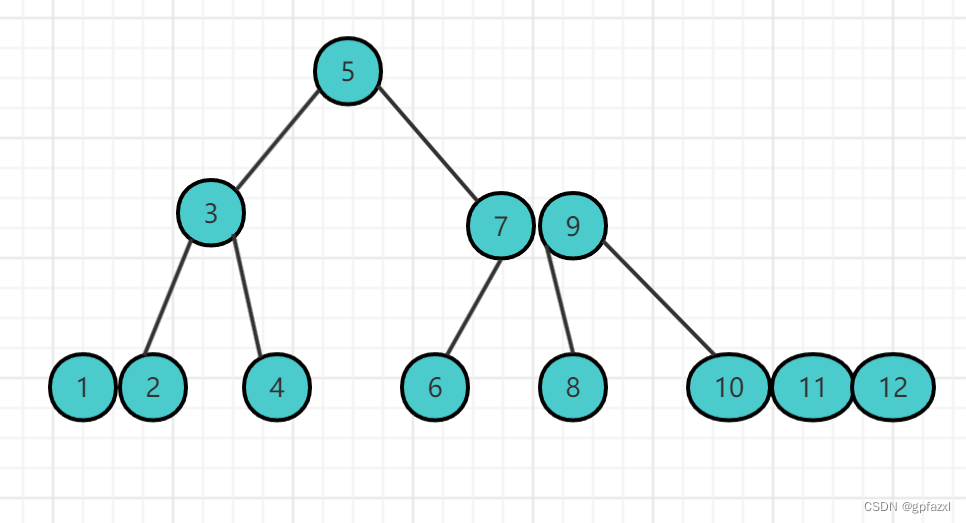
2 生成的过程
接下来我们通过演示来看看2-3-4树生成的过程
第一次插入—2节点
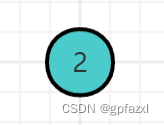
插入第二个节点–3节点 合并
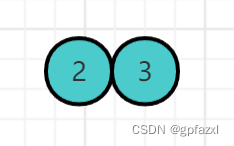
插入第三个节点—4节点 合并
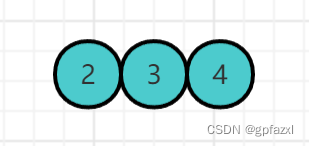
插入第四个节点—5节点 需要分裂
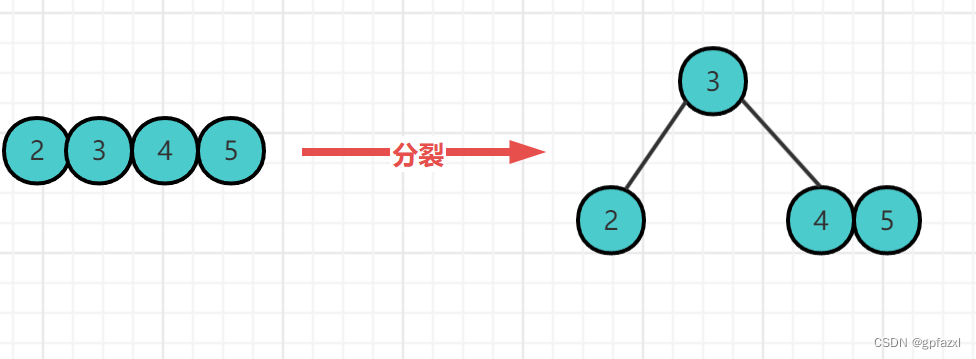
插入6
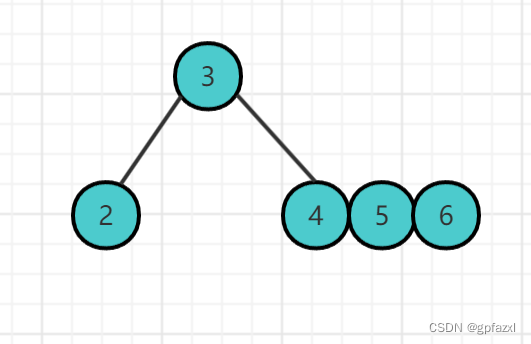
插入7
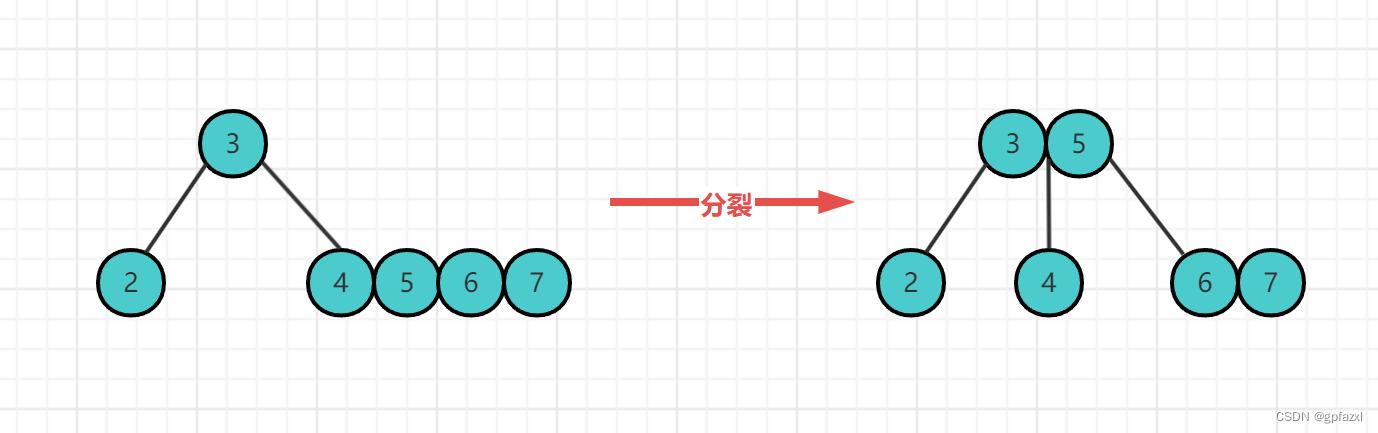
插入8
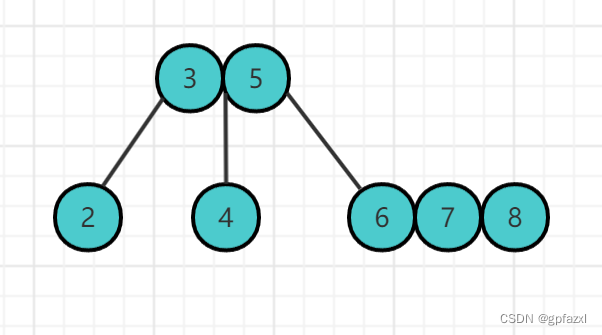
插入9

插入10
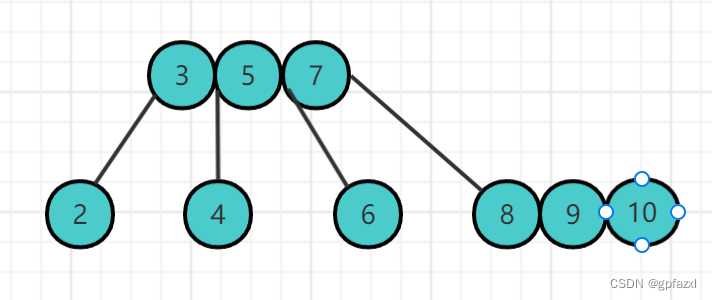
插入11
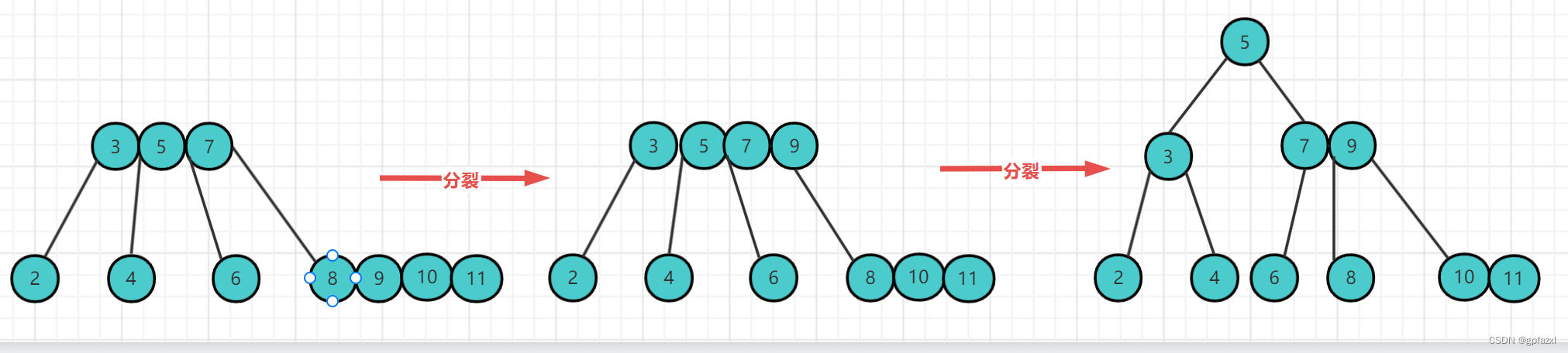
插入12

最后我们插入1来看看效果
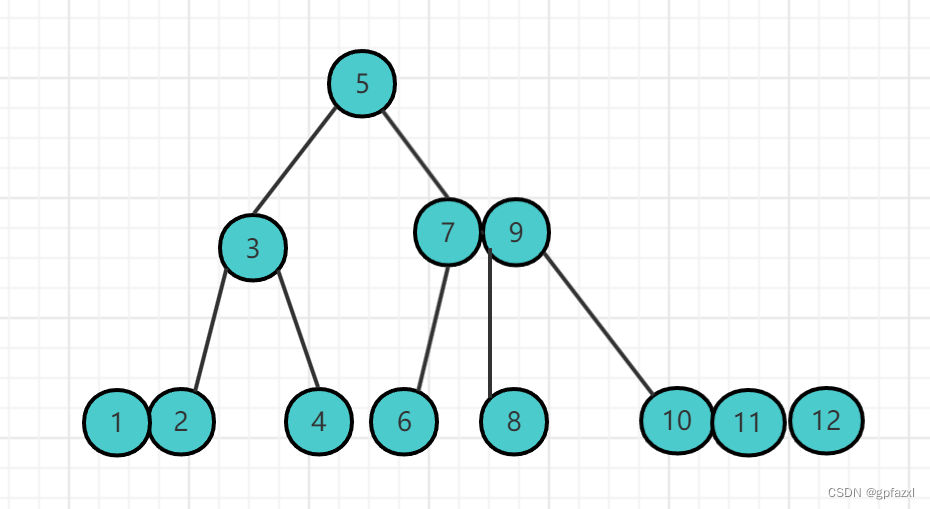
到这儿相信大家对于2-3-4树应该有了个直观的认知了。
3 和红黑树的等价关系
红黑树起源于2-3-4树,它的本质就是2-3-4树。
3.1 2节点
一个2节点对应的红黑树节点就是一个黑色节点

3.2 3节点
一个三节点可以有两种情况的红黑树节点,一种是右倾,一种是左倾,所以一个2-3-4树可以有多个红黑树
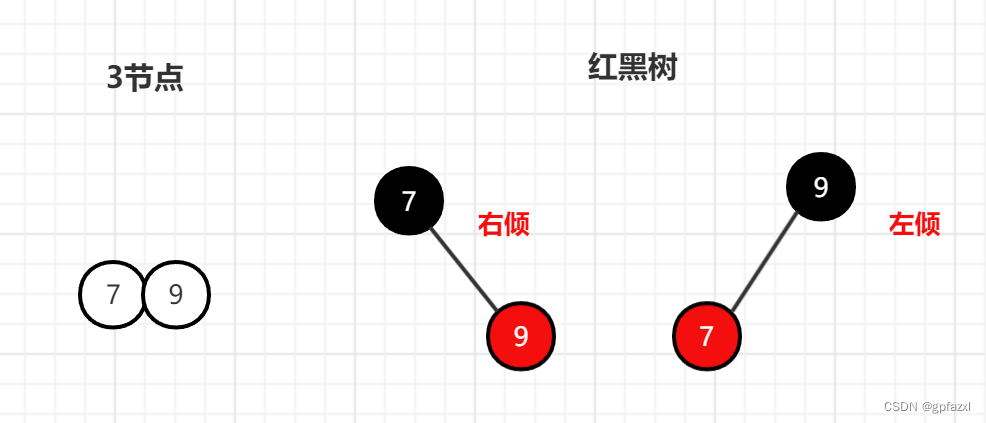
原则:上黑下红
3.3 4节点
一个四节点转换的情况只有一种,中间节点黑色,左右节点红色
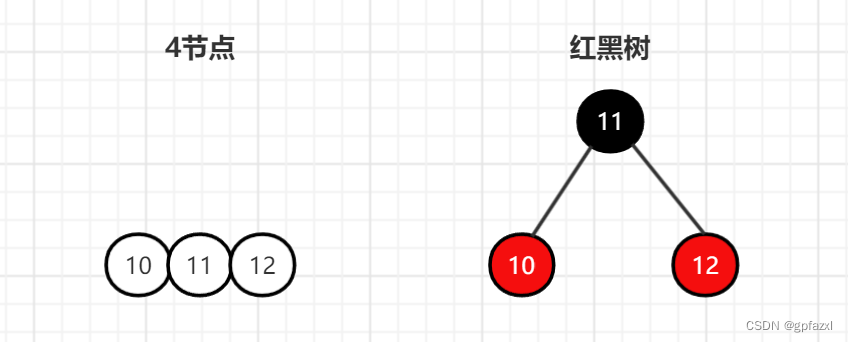
3.4 裂变状态
还有就是在2-3-4树中存在的裂变状态。转换为红黑树后会先变色(不能有两个相邻的红色节点)。
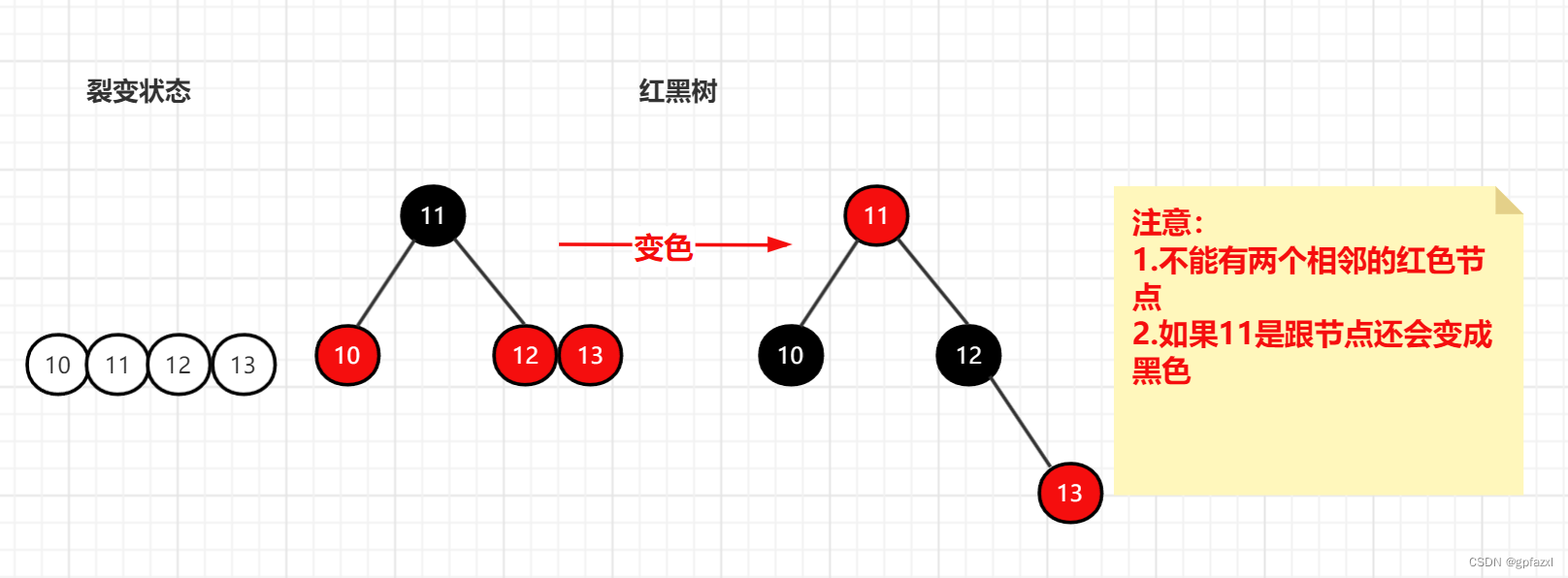
4 转换为红黑树
接下来具体看看一个2-3-4树是如何转换为对应的红黑树的,
原始的2-3-4树:

按照右倾规则来转换为:
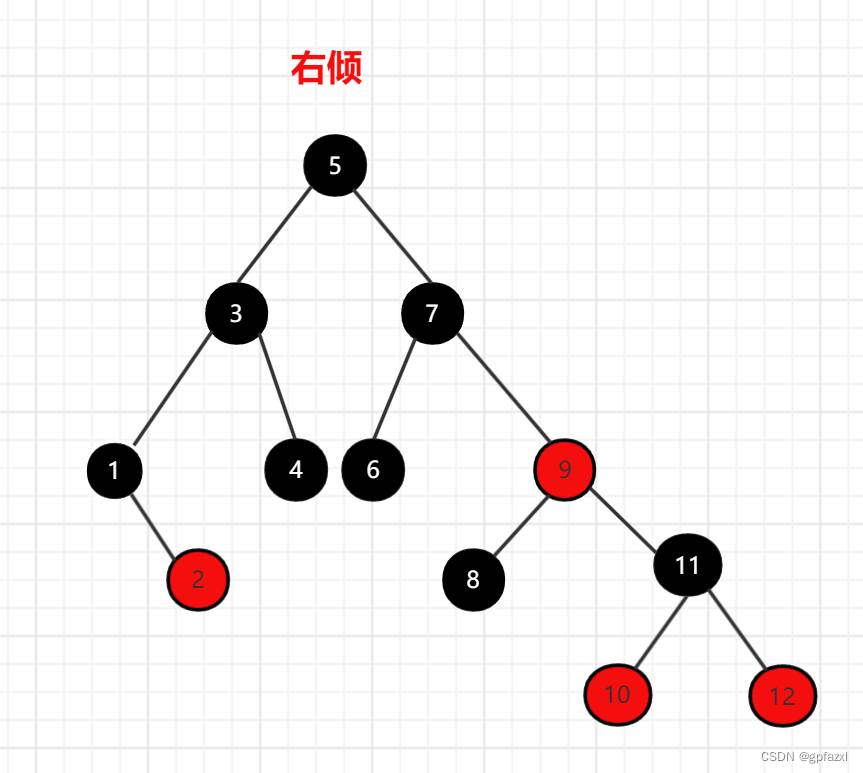
转换后满足黑色节点平衡的要求
按照左倾规则来转换为:
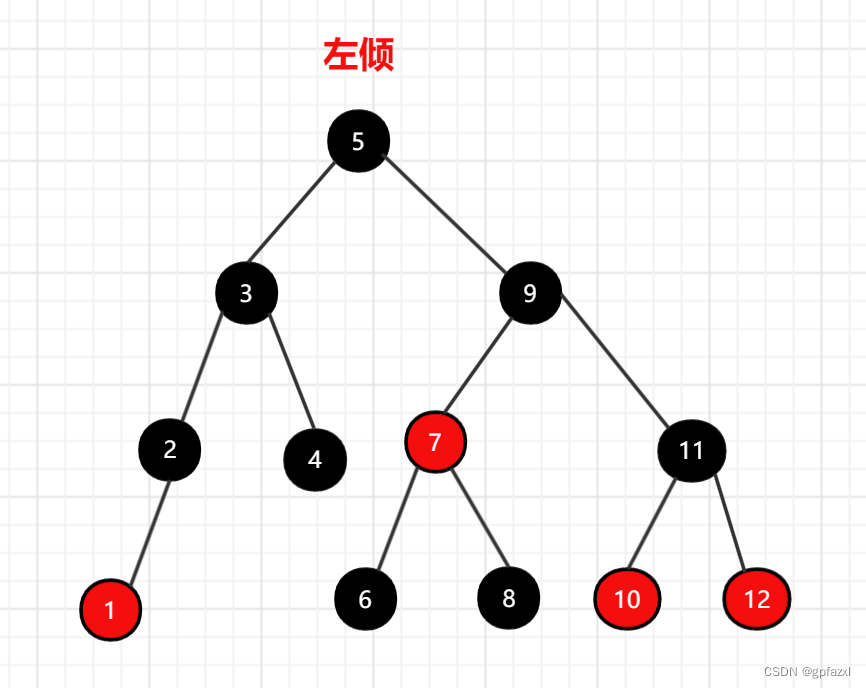
2.2 堆
2.3 图
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若内容造成侵权/违法违规/事实不符,请联系邮箱:jacktools123@163.com进行投诉反馈,一经查实,立即删除!
标签:

