首页 > 基础资料 博客日记
Java蓝桥杯
2024-03-07 10:00:05基础资料围观848次

目录
往年真题
2023年第十四届蓝桥杯大赛软件类省赛Java研究生组真题 - 题库 - C语言网
2022年第十三届蓝桥杯大赛软件类决赛Java研究生组真题 - 题库 - C语言网
2021年蓝桥杯第十二届省赛及国赛真题 - 题库 - C语言网
2020年蓝桥杯第十一届省赛及国赛真题 - 题库 - C语言网
2019年蓝桥杯第十届省赛及国赛真题 - 题库 - C语言网
2018年蓝桥杯第九届省赛及国赛真题 - 题库 - C语言网
2017年蓝桥杯第八届省赛及国赛真题 - 题库 - C语言网
2016年蓝桥杯第七届省赛及国赛真题 - 题库 - C语言网
2015年蓝桥杯第六届省赛及国赛真题 - 题库 - C语言网
2014年蓝桥杯第五届省赛及国赛真题 - 题库 - C语言网
2013年蓝桥杯第四届省赛及国赛真题 - 题库 - C语言网
题目分类
搜索
1. 全排列
输出自然数1到n所有不重复的排列,即n的全排列。
代码:
import java.util.*;
public class Main {
static int n;
static boolean[] visit;
static int[] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
arr = new int[n+1];
visit = new boolean[n+1];
dfs(1);
}
public static void dfs(int index) {
if (index == n+1) {
for (int i = 1; i <= n; i++) {
System.out.print(" "+arr[i]);
}
System.out.println();
return;
}
for (int i = 1; i <= n; i++) {
if (!visit[i]) {
arr[index] = i;
visit[i] = true;
dfs(index+1);
visit[i] = false;
}
}
}
}2. 跳马
一个8×8的棋盘上有一个马初始位置为(a,b),他想跳到(c,d),问是否可以?如果可以,最少要跳几步?
输入格式
一行四个数字a,b,c,d。
输出格式
如果跳不到,输出-1;否则输出最少跳到的步数。
样例输入
1 1 2 3
样例输出
1
数据规模和约定
0<a,b,c,d≤8且都是整数。
代码:
import java.util.*;
public class Main {
static int n = 8;
static int a,b,c,d;
static boolean[][] visit;
//马走日,一共有8种移动
static int[][] action = {{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
static int min_step = 100;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
a = sc.nextInt();
b = sc.nextInt();
c = sc.nextInt();
d = sc.nextInt();
visit = new boolean[n+1][n+1];
visit[a][b] = true;
dfs(a, b, 0);
if (min_step == 100) {
System.out.print(-1);
}
else {
System.out.print(min_step);
}
}
public static void dfs(int x,int y,int step) {
//剪枝,如果该点的步数比之前到该点步数大,不必进行后续操作
if (step > min_step) {
return;
}
if (x == c && y == d) {
min_step = Math.min(min_step, step);
return;
}
for (int i = 0; i < n; i++) {
int x_new = x + action[i][0];
int y_new = y + action[i][1];
if (x_new >0 && x_new <= n && y_new >0 && y_new <= n) {
visit[x_new][y_new] = true;
dfs(x_new, y_new,step+1);
visit[x_new][y_new] = false;
}
}
}
}3. 粘木棍
有N根木棍,需要将其粘贴成M个长木棍,使得最长的和最短的的差距最小。
输入格式
第一行两个整数N,M。
一行N个整数,表示木棍的长度。
输出格式
一行一个整数,表示最小的差距
样例输入
3 2
10 20 40
样例输出
10
数据规模和约定
N, M<=7
代码:
import java.util.*;
public class Main {
static int n,m;
//记录初始木棍长度
static int[] arr;
//记录粘贴后的木棍长度
static int[] sum;
//记录某根木棍是否使用
static boolean[] visit;
static int res = 0x3f3f3f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n+1];
sum = new int[n+1];
visit = new boolean [n+1];
for (int i = 1; i <= n; i++) {
arr[i] = sc.nextInt();
}
dfs(1);
System.out.print(res);
}
public static void dfs(int k) {
//所有木棍均已使用
if (k > n) {
int max = sum[1];
int min = sum[1];
for (int i = 1; i <= m; i++) {
max = Math.max(max, sum[i]);
min = Math.min(min, sum[i]);
}
res = Math.min(max-min, res);
return;
}
for (int i = k; i <= n; i++) {
if (!visit[i]) {
//使用第i根
visit[i] = true;
for (int j = 1; j <= m; j++) {
sum[j] += arr[i];
dfs(k+1);
sum[j] -= arr[i];
}
visit[i] = false;
}
}
}
}4. 24点
24点游戏是一个非常有意思的游戏,很流行,玩法很简单:给你4张牌,每张牌上有数字(其中A代表1,J代表11,Q代表12,K代表13),你可以利用数学中的加、减、乘、除以及括号想办法得到24,例如:
((A*K)-J)*Q等价于((1*13)-11)*12=24
加减乘不用多说了,但除法必须满足能整除才能除!这样有一些是得不到24点的,所以这里只要求求出不超过24的最大值。
输入格式
输入第一行N(1<=N<=5)表示有N组测试数据。每组测试数据输入4行,每行一个整数(1到13)表示牌值。
输出格式
每组测试数据输出一个整数,表示所能得到的最大的不超过24的值。
样例输入
3
3
3
3
3
1
1
1
1
12
5
13
1
样例输出
24
4
21
代码:
import java.util.*;
public class Main {
static int res = 0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] arr = new int[n+1][5];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= 4; j++) {
arr[i][j] = sc.nextInt();
}
}
for (int i = 1; i <= n; i++) {
dfs(arr[i],4);
System.out.println(res);
res = 0;
}
}
public static void dfs(int[] arr,int n) {
if (n==1) {
if (arr[n] <= 24) {
res = Math.max(res, arr[n]);
}
return;
}
//将两个数进行运算
for (int i = 1; i < n; i++) {
for (int j = i+1; j <= n; j++) {
int a = arr[i];
int b = arr[j];
//加法
arr[j] = a+b;
arr[i] = arr[n];
dfs(arr, n-1);
//乘法
arr[j] = a*b;
arr[i] = arr[n];
dfs(arr, n-1);
//减法1
arr[j] = a-b;
arr[i] = arr[n];
dfs(arr, n-1);
//减法2
arr[j] = b-a;
arr[i] = arr[n];
dfs(arr, n-1);
//除法
if (b != 0 && a%b == 0) {
arr[j] = a/b;
arr[i] = arr[n];
dfs(arr, n-1);
}
if (a != 0 && b%a == 0) {
arr[j] = b/a;
arr[i] = arr[n];
dfs(arr, n-1);
}
arr[i] = a;
arr[j] = b;
}
}
}
}5. 自然数拆分
HJQ同学发现了一道数学题,要求n拆分成若干自然数和的方案
输入格式
输入n
输出格式
输出n拆分成若干自然数和的方案,每个方案一行
数据规模和约定
n <= 10
代码:
import java.util.*;
public class Main {
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
List<Integer> list = new ArrayList<Integer>();
dfs(1, list);
}
public static void dfs(int start, List<Integer> list) {
if (sum(list) == n) {
for (int i = 0; i < list.size(); i++) {
if (i != list.size()-1) {
System.out.print(list.get(i)+"+");
}
else {
System.out.println(list.get(i));
}
}
return;
}
if (sum(list) > n) {
return;
}
for (int i = start; i < n; i++) {
//从start开始保证由小到大输出
list.add(i);
//防止出现数相同但顺序不同的情况
dfs(i, list);
list.remove(list.size()-1);
}
}
public static int sum(List<Integer> list) {
int sum = 0;
for (int i = 0; i < list.size(); i++) {
sum += list.get(i);
}
return sum;
}
}6. 最大数字
给定一个正整数 N 。你可以对N 的任意一位数字执行任意次以下 2 种操 作:
- 将该位数字加 1 。如果该位数字已经是 9 , 加 1 之后变成 0 。
- 将该位数字减 1 。如果该位数字已经是 0 , 减 1 之后变成 9 。
你现在总共可以执行 1 号操作不超过 A 次, 2 号操作不超过 B 次。 请问你最大可以将 N 变成多少?
输入格式
第一行包含 3 个整数: N,A,B 。
输出格式
一个整数代表答案。
样例输入
123 1 2
样例输出
933
样例说明
对百位数字执行 2 次 2 号操作, 对十位数字执行 1 次 1 号操作。
评测用例规模与约定
1≤N≤1017;0≤A,B≤100
代码:
import java.util.*;
public class Main {
static int cnt1,cnt2;
static String n;
static long res;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.next();
cnt1 = sc.nextInt();
cnt2 = sc.nextInt();
dfs(0, 0);
System.out.print(res);
}
public static void dfs(int i, long value) {
if (i < n.length()) {
int x = n.charAt(i)-'0';
int t = Math.min(cnt1, 9-x);
cnt1 -= t;
dfs(i+1, value*10+x+t);
cnt1 += t;
if (cnt2 > x) {
cnt2 = cnt2-x-1;
dfs(i+1, value*10+9);
cnt2 = cnt2+x+1;
}
}
else {
res = Math.max(res, value);
}
}
}7. 分考场
n个人参加某项特殊考试。为了公平,要求任何两个认识的人不能分在同一个考场。求最少需要分几个考场才能满足条件。
输入格式
第一行,一个整数n(1<n<100),表示参加考试的人数。
第二行,一个整数m,表示接下来有m行数据
以下m行每行的格式为:两个整数a,b,用空格分开 (1<=a,b<=n) 表示第a个人与第b个人认识。
输出格式
一行一个整数,表示最少分几个考场。
样例输入
5
8
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5
样例输出
4
代码:
import java.util.*;
public class Main {
static boolean[][] arr;
static int[][] place;
static int n,num;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int m = sc.nextInt();
arr = new boolean[n+1][n+1];
place = new int[n+1][n+1];
num = n;
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
arr[a][b] = true;
arr[b][a] = true;
}
dfs(1,1);
System.out.print(num);
}
public static void dfs(int id, int classes) {
//剪枝,考场数大于最小考场数
if (classes >= num) {
return;
}
//安排了n个人
if (id > n) {
num = Math.min(num, classes);
return;
}
//初始化考场号和考场位置
for (int classNumber = 1; classNumber <= classes; classNumber++) {
//把id号学生放入classNumber号考场
int classPosition = 1;
//如果classNumber号考场的classPosition有人,且不认识id号学生
while(place[classNumber][classPosition]!=0 && !arr[id][place[classNumber][classPosition]]) {
classPosition++;
}
//如果没人坐则安排入座
if (place[classNumber][classPosition]==0) {
place[classNumber][classPosition] = id;
dfs(id+1, classes);
//回溯
place[classNumber][classPosition] = 0;
}
}
//如果1至classes考场都不能满足,则新开考场
place[classes+1][1] = id;
dfs(id+1, classes+1);
//回溯
place[classes+1][1] = 0;
}
}8. 长草
小明有一块空地,他将这块空地划分为 n 行 m 列的小块,每行和每列的长度都为 1。小明选了其中的一些小块空地,种上了草,其他小块仍然保持是空地。这些草长得很快,每个月,草都会向外长出一些,如果一个小块种了草,则它将向自己的上、下、左、右四小块空地扩展,这四小块空地都将变为有草的小块。请告诉小明,k 个月后空地上哪些地方有草。
输入格式
输入的第一行包含两个整数 n, m。接下来 n 行,每行包含 m 个字母,表示初始的空地状态,字母之间没有空格。如果为小数点,表示为空地,如果字母为 g,表示种了草。接下来包含一个整数 k。
输出格式
输出 n 行,每行包含 m 个字母,表示 k 个月后空地的状态。如果为小数点,表示为空地,如果字母为 g,表示长了草。
样例输入
4 5
.g...
.....
..g..
.....
2
样例输出
gggg.
gggg.
ggggg
.ggg.
代码:
import java.util.*;
public class Main {
public static class Node {
int x;
int y;
public Node(int x,int y) {
this.x = x;
this.y = y;
}
}
static int n,m;
static char[][] arr;
static int[][] d = {{1,0},{-1,0},{0,1},{0,-1}};
static Queue<Node> queue = new LinkedList<>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new char[n][m];
for (int i = 0; i < n; i++) {
arr[i] = sc.next().toCharArray();
}
int k = sc.nextInt();
//遍历将有草的位置放入队列
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (arr[i][j] == 'g') {
queue.offer(new Node(i, j));
}
}
}
while(k > 0) {
k--;
bfs();
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
System.out.print(arr[i][j]);
}
System.out.println();
}
}
public static void bfs() {
int len = queue.size();
while (len > 0) {
len--;
Node node = queue.poll();
//向四个方向长草
for (int i = 0; i < 4; i++) {
int nx = node.x + d[i][0];
int ny = node.y + d[i][1];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && arr[nx][ny] == '.') {
queue.offer(new Node(nx, ny));
arr[nx][ny] = 'g';
}
}
}
}
}9. 青蛙跳杯子
X星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。X星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个里边有一只青蛙。
*WWWBBB
其中,W字母表示白色青蛙,B表示黑色青蛙,表示空杯子。X星的青蛙很有些癖好,它们只做3个动作之一:
1. 跳到相邻的空杯子里。
2. 隔着1只其它的青蛙(随便什么颜色)跳到空杯子里。
3. 隔着2只其它的青蛙(随便什么颜色)跳到空杯子里。
对于上图的局面,只要1步,就可跳成下图局面:
WWW*BBB
本题的任务就是已知初始局面,询问至少需要几步,才能跳成另一个目标局面。输入为2行,2个串,表示初始局面和目标局面。输出要求为一个整数,表示至少需要多少步的青蛙跳。
输入描述
输入为 2 行,2 个串,表示初始局面和目标局面。我们约定,输入的串的长度不超过 15。
输出描述
输出要求为一个整数,表示至少需要多少步的青蛙跳。
样例输入
*WWBB
WWBB*
样例输出
2
代码:
import java.util.*;
public class Main {
static Queue<String> queue = new LinkedList<String>();
//记录到达当前状态需要几步
static Map<String, Integer> map = new HashMap<String, Integer>();
static int[] d = {-3,-2,-1,1,2,3};
static int step;
static String start,target;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
start = sc.next();
target = sc.next();
queue.offer(start);
bfs();
}
public static void bfs() {
while(queue.size() > 0) {
int len = queue.size();
step++;
while(len > 0) {
len--;
String s = queue.poll();
if (s.equals(target)) {
System.out.println(map.get(s));
return;
}
//将每一只青蛙在六个方向上
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) != '*') {
char c = s.charAt(i);
for (int j = 0; j < d.length; j++) {
int newc = d[j] + i;
if (newc >= 0 && newc < s.length() && s.charAt(newc) == '*') {
//跳跃更新位置
StringBuilder sb = new StringBuilder(s);
sb.setCharAt(i, '*');
sb.setCharAt(newc, c);
String newString = sb.toString();
if (!map.containsKey(newString)) {
map.put(newString, step);
queue.offer(newString);
}
}
}
}
}
}
}
}
}10. 卡片换位
你玩过华容道的游戏吗?这是个类似的,但更简单的游戏。看下面 3 x 2 的格子
+---+---+---+
| A | * | * |
+---+---+---+
| B | | * |
+---+---+---+
在其中放 5 张牌,其中 A 代表关羽,B 代表张飞,* 代表士兵。还有个格子是空着的。你可以把一张牌移动到相邻的空格中去(对角不算相邻)。游戏的目标是:关羽和张飞交换位置,其它的牌随便在哪里都可以。
输入描述
输入两行 6 个字符表示当前的局面
输出描述
一个整数,表示最少多少步,才能把 A B 换位(其它牌位置随意)
样例输入
* A
**B
样例输出
17
代码:
import java.util.*;
public class Main {
static String start;
static int[][] d= {{1,0},{-1,0},{0,1},{0,-1}};
static Queue<String> queue = new LinkedList<String>();
//记录到达当前状态的步数
static HashMap<String, Integer> map = new HashMap<String, Integer>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String string1 = sc.nextLine();
String string2 = sc.nextLine();
start = string1+string2;
bfs();
}
public static void bfs() {
map.put(start, 0);
queue.offer(start);
//获取A,B在字符串中的位置
int a = 0, b = 0;
for (int i = 0; i < start.length(); i++) {
if (start.charAt(i) == 'A') {
a = i;
}
if (start.charAt(i) == 'B') {
b = i;
}
}
while(!queue.isEmpty()) {
String string = queue.poll();
//判断是否符合
if (string.charAt(a) == 'B' && string.charAt(b) == 'A') {
System.out.print(map.get(string));
return;
}
//查找空格在字符串的位置
int index = string.indexOf(' ');
int x = index/3;
int y = index%3;
//四个方向可以向空格移动
for (int i = 0; i < 4; i++) {
int nx = x + d[i][0];
int ny = y + d[i][1];
if (nx >= 0 && nx < 2 && ny >= 0 && ny < 3) {
//交换位置
char[] c = string.toCharArray();
c[index] = c[nx*3+ny];
c[nx*3+ny] = ' ';
String newString = new String(c);
if (!map.containsKey(newString)) {
map.put(newString, map.get(string)+1);
queue.offer(newString);
}
}
}
}
}
}11. 移动字母
2x3=6 个方格中放入 ABCDE 五个字母,右下角的那个格空着。如下图所示。

和空格子相邻的格子中的字母可以移动到空格中,比如,图中的 C 和 E 就可以移动,移动后的局面分别是:
A B
D E C
A B C
D E
为了表示方便,我们把 6 个格子中字母配置用一个串表示出来,比如上边的两种局面分别表示为:
AB*DEC
ABCD*E
题目的要求是:请编写程序,由用户输入若干表示局面的串,程序通过计算,输出是否能通过对初始状态经过若干次移动到达该状态。可以实现输出 1,否则输出 0。初始状态为:ABCDE*。
输入描述
先是一个整数 n,表示接下来有 n 行状态。
输出描述
程序输出 n 行 1 或 0。
样例输入
3
ABCDE*
AB*DEC
CAED*B
样例输出
1
1
0
代码:
import java.util.*;
public class Main {
static int n;
static String start = "ABCDE*", target;
static int[][] d= {{1,0},{-1,0},{0,1},{0,-1}};
static Queue<String> queue;
static HashSet<String> set;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 0; i < n; i++) {
target = sc.next();
bfs();
}
}
public static void bfs() {
queue = new LinkedList<String>();
set = new HashSet<String>();
queue.add(start);
set.add(start);
while (!queue.isEmpty()) {
String string = queue.poll();
//判断是否符合
if (string.equals(target)) {
System.out.println(1);
return;
}
//查找空格的位置
int index = string.indexOf('*');
int x = index/3;
int y = index%3;
//四个方向移动
for (int i = 0; i < d.length; i++) {
int nx = x + d[i][0];
int ny = y + d[i][1];
if (nx >= 0 && nx < 2 && ny >= 0 && ny < 3) {
//交换位置
char[] c = string.toCharArray();
c[index] = c[nx*3+ny];
c[nx*3+ny] = '*';
String nstring = new String(c);
if (!set.contains(nstring)) {
set.add(nstring);
queue.add(nstring);
}
}
}
}
System.out.println(0);
}
}动态规划
1. 01背包问题

f[i][j]在i个物品中,选取容量为j的物品的价值。第i个物品只有两种情况,拿或者不拿。如f[4][8],不拿第4个,当前价值为在其他3个里选取容量为8的物品,即f[3][8];如果拿第4个,则在其他3个里选取容量为8-value[4] = 3的物品,当前价值为f[3][3]+v[4]。只需要比较两种情况哪个价值更大,选取哪个。
f[4][8] = Max(f[3][8],f[3][8-5]+v[4])
状态转移公式:
f[i][j]= Max(f[i-1][j],f[i-1][j-w[i]]+v[i])
2. 质数拆分
将 2019拆分为若干个两两不同的质数之和,一共有多少种不同的方法? 注意交换顺序视为同一种方法,例如 2+2017=2019 与 2017+2=2019 视为同一种方法。
代码:
import java.util.*;
/*
* dp[i][j]使用i个素数达到和为j的情况数量
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int index = 1;
int[] arr = new int[400];
long[][] dp = new long[400][2020];
for(int i=1;i<2019;i++) {
if(isPrime(i)) {
arr[index++] = i;
}
}
dp[0][0] = 1;
for(int i=1;i<index;i++) {
for(int j=0;j<=2019;j++) {
if(j<arr[i]) {
dp[i][j] = dp[i-1][j];
}
else {
dp[i][j] = dp[i-1][j]+dp[i-1][j-arr[i]];
}
}
}
System.out.print(dp[index-1][2019]);
}
public static boolean isPrime(int n) {
if(n==1) {
return false;
}
for(int i=2;i<=Math.sqrt(n);i++) {
if(n%i == 0) {
return false;
}
}
return true;
}
}3. 秘密行动
小D接到一项任务,要求他爬到一座n层大厦的顶端与神秘人物会面。这座大厦有一个神奇的特点,每层的高度都不一样,同时,小D也拥有一项特殊能力,可以一次向上跳跃一层或两层,但是这项能力无法连续使用。已知向上1高度消耗的时间为1,跳跃不消耗时间。由于事态紧急,小D想知道他最少需要多少时间到达顶层。
输入格式
第一行包含一个整数n,代表楼的高度。接下来n行每行一个整数ai,代表i层的楼层高度(ai <= 100)。
输出格式
输出1行,包含一个整数,表示所需的最短时间。
样例输入
5
3
5
1
8
4
样例输出
1
代码:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n+1];
int[][] dp = new int[n+1][2];
//dp[][0]代表爬,dp[][1]代表跳
for(int i=1;i<=n;i++) {
arr[i] = sc.nextInt();
}
dp[0][0] = dp[0][1] = 0;
dp[1][0] = arr[1];
for(int i=2;i<n+1;i++) {
//爬,上一次可以是爬或者跳
dp[i][0] = Math.min(dp[i-1][0]+arr[i], dp[i-1][1]+arr[i]);
//跳,上一次只能是爬
dp[i][1] = Math.min(dp[i-2][0], dp[i-1][0]);
}
System.out.println(Math.min(dp[n][0], dp[n][1]));
}
}4. 第二点五个不高兴的小明
有一条长为n的走廊,小明站在走廊的一端,每次可以跳过不超过p格,每格都有一个权值wi。小明要从一端跳到另一端,不能回跳,正好跳t次,请问他跳过的方格的权值和最大是多少?
输入格式
输入的第一行包含两个整数n, p, t,表示走廊的长度,小明每次跳跃的最长距离和小明跳的次数。
接下来n个整数,表示走廊每个位置的权值。
输出格式
输出一个整数。表示小明跳过的方格的权值和的最大值。
样例输入
8 5 3
3 4 -1 -100 1 8 7 6
样例输出
12
数据规模和约定
1<=n, p, t<=1000, -1000<=wi<=1000。
代码:
import java.util.*;
/* 0 1 2 3 . . . . n n+1
* 0 3 4 -1 -100 1 8 7 6 0
* dp[i][j]跳到第i格跳了j次的价值和
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int p = sc.nextInt();
int t = sc.nextInt();
int[] w = new int[n+2];
int[][] dp = new int[n+2][n+2];
for(int i=1;i<=n;i++) {
w[i] = sc.nextInt();
}
for(int i=0;i<n+2;i++) {
Arrays.fill(dp[i], -0x3f3f3f);
}
for(int i=1;i<=p&&i<=n+1;i++) {
dp[i][1] = w[i];
}
for(int i=1;i<=n+1;i++) {
for(int j=2;j<=t;j++) {
//跳k格
for(int k=1;k<=p&&k<=i;k++) {
dp[i][j] = Math.max(dp[i][j], dp[i-k][j-1]+w[i]);
}
}
}
System.out.println(dp[n+1][t]);
}
}5. 和谐宿舍2
我的某室友学过素描,墙上有n张他的作品。这些作品都是宽度为1,高度不定的矩形,从左到右排成一排,且底边在同一水平线上。宿舍评比就要来了,为了及格,我们决定买不多于m块的矩形木板,把这些作品和谐掉。要求木板也从左到右排成一排,且底边与作品的底边在同一水平线上。在能够把所有作品和谐掉的前提下,我们希望这些木板的面积和最小,问最小面积和。
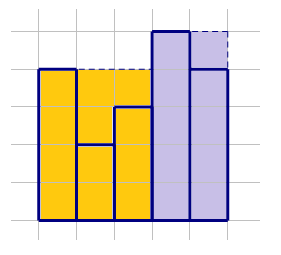
输入格式
第一行两个数n和m,表示作品数和木板数;第二行n个数Hi,表示从左到右第i个作品的高度。
输出格式
一行一个数ans,表示答案。
样例输入
5 2
4 2 3 5 4
样例输出
22
数据规模和约定
对于30%的数据:1<=n,m<=10;对于100%的数据:1<=n,m<=100,1<=Hi<=10000。
代码:
import java.util.*;
/*
* dp[i][j] 用j块板来挡前i张作品
* max[i][j] 第i到第j作品的最大高度
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int INF = 0x3f3f3f;
int[] arr = new int[n+1];
int[][] max = new int[n+1][n+1];
int[][] dp = new int[n+1][n+1];
for(int i=1;i<=n;i++) {
arr[i] = sc.nextInt();
}
//求i到j作品的最大高度
for(int i=1;i<=n;i++) {
for(int j=i;j<=n;j++) {
max[i][j] = Math.max(max[i][j-1], arr[j]);
}
}
for(int i=0;i<=n;i++) {
Arrays.fill(dp[i], INF);
}
//只有一块板的时候
for(int i=1;i<=n;i++) {
dp[i][1] = max[1][i]*i;
}
for(int i=1;i<=n;i++) {
for(int j=2;j<=m && j<=i;j++) {
//遍历木板的宽度
for(int k=1;k<=i-j+1;k++) {//j-1<=i-k
dp[i][j] = Math.min(dp[i][j], dp[i-k][j-1]+max[i-k+1][i]*k);
}
}
}
System.out.println(dp[n][m]);
}
}6. 最大值路径
刷微博,编程序。如下图所示,@北京发布 提出了如下“头脑震荡”问题。对此问题做一般化描述:
有n阶方阵,从矩阵的左下角元素为起点,从行或列(水平或垂直)两个方向上移动,直到右上角。求出有多少条路径可以使得经过的元素累加值最大,最大值是多少。
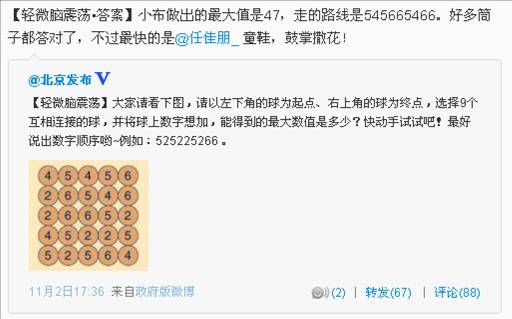
输入格式
共有n+1行。
第一行整数n,表示矩阵的阶数,2<=n<=10。第二行起,每行n个整数,以空格分隔,共n行。
输出格式
一行,两个空格分隔的数,第一个表示最大值路径的条数,第二个表示最大值。
样例输入
5
4 5 4 5 6
2 6 5 4 6
2 6 6 5 2
4 5 2 2 5
5 2 5 6 4
样例输出
3 47
代码:
import java.util.*;
/*
* dp[i][j] 到达当前(i,j)点的最大值和
*/
public class Main {
static int[][] dp;
static int cnt=1;
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int[][] arr = new int[n][n];
dp = new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
arr[i][j] = sc.nextInt();
}
}
for(int i=0;i<n;i++) {
Arrays.fill(dp[i], -0x3f3f3f);
}
dp[n-1][0] = arr[n-1][0];
//将最左侧一列初始化
for(int i=n-2;i>=0;i--) {
dp[i][0] = dp[i+1][0]+arr[i][0];
}
//将最下面一行初始化
for(int j=1;j<n;j++) {
dp[n-1][j] = dp[n-1][j-1]+arr[n-1][j];
}
//遍历到达每个点的最大值
for(int i=n-2;i>=0;i--) {
for(int j=1;j<n;j++) {
//只能从(i+1,j)和(i,j-1)两个点到达(i,j),取大的值加上(i,j)当前的值
dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1])+arr[i][j];
}
}
System.out.println(dfs(0,n-1)+" "+dp[0][n-1]);
}
//回溯遍历寻找最大路径
public static int dfs(int x,int y) {
//如果在边缘,则不需再判断,因为后面只有一条直的路径
if(x!=n-1 && y!=0) {
//两条路径都为最大的路径
if(dp[x][y-1] == dp[x+1][y]) {
cnt++;
dfs(x,y-1);
dfs(x+1,y);
}
//dp[x][y-1]为最大的路径
if(dp[x][y-1] > dp[x+1][y]) {
dfs(x,y-1);
}
//dp[x+1][y]为最大的路径
if(dp[x][y-1] < dp[x+1][y]) {
dfs(x+1,y);
}
}
return cnt;
}
}7. 矩阵乘法
有n个矩阵,大小分别为a0*a1, a1*a2, a2*a3, ..., a[n-1]*a[n],现要将它们依次相乘,只能使用结合率,求最少需要多少次运算。两个大小分别为p*q和q*r的矩阵相乘时的运算次数计为p*q*r。
输入格式
输入的第一行包含一个整数n,表示矩阵的个数。第二行包含n+1个数,表示给定的矩阵。
输出格式
输出一个整数,表示最少的运算次数。
样例输入
3
1 10 5 20
样例输出
150
数据规模和约定
1<=n<=1000, 1<=ai<=10000。
代码:
import java.util.*;
/*
* dp[i][j] 第i到j个矩阵之间运算次数
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
long[] arr = new long[n+1];
long[][] dp = new long[n+1][n+1];
for(int i=0;i<=n;i++) {
arr[i] = sc.nextInt();
}
for(int i=0;i<=n;i++) {
Arrays.fill(dp[i], (long) 1e18);
}
for(int i=1;i<=n;i++) {
dp[i][i] = 0;
}
for(int l=1;l<=n;l++) {//k表示dp数组中横纵坐标之差
for(int i=1;i<=n-l;i++) {
int j = i+l;
for(int k=i;k<j;k++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k+1][j]+arr[i-1]*arr[k]*arr[j]);
}
}
}
System.out.println(dp[1][n]);
}
}8. 合并石子
在一条直线上有n堆石子,每堆有一定的数量,每次可以将两堆相邻的石子合并,合并后放在两堆的中间位置,合并的费用为两堆石子的总数。求把所有石子合并成一堆的最小花费。
输入格式
输入第一行包含一个整数n,表示石子的堆数。
接下来一行,包含n个整数,按顺序给出每堆石子的大小 。
输出格式
输出一个整数,表示合并的最小花费。
样例输入
5
1 2 3 4 5
样例输出
33
数据规模和约定
1<=n<=1000, 每堆石子至少1颗,最多10000颗。
代码:
import java.util.*;
/*
* dp[i][j] 第i到j堆石子的最小花费
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n+1];
int[] sum = new int[n+1];
long[][] dp = new long[n+1][n+1];
for(int i=1;i<=n;i++) {
arr[i] = sc.nextInt();
}
for(int i=1;i<=n;i++) {
Arrays.fill(dp[i], (long) 1e18);
}
for(int i=1;i<=n;i++) {
dp[i][i] = 0;
sum[i] = sum[i-1] + arr[i];
}
for(int l=1;l<=n;l++) {
for(int i=1;i<=n-l;i++) {
int j = i+l;
for(int k=i;k<j;k++) {
dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
}
}
}
System.out.println(dp[1][n]);
}
}9. 拿糖果
妈妈给小B买了N块糖!但是她不允许小B直接吃掉。假设当前有M块糖,小B每次可以拿P块糖,其中P是M的一个不大于根号下M的质因数。这时,妈妈就会在小B拿了P块糖以后再从糖堆里拿走P块糖。然后小B就可以接着拿糖。现在小B希望知道最多可以拿多少糖。
输入格式
一个整数N
输出格式
最多可以拿多少糖
样例输入
15
样例输出
6
数据规模和约定
N <= 100000
代码:
import java.util.*;
/*
* dp[i] i块糖中可以最多拿的数量
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] dp = new int[n+1];
for(int i=2+2;i<=n;i++) {
for(int p=2;p*p<=i;p++) {
//是质因数
if(i%p==0 && IsPrime(p)) {
dp[i] = Math.max(dp[i], p+dp[i-p-p]);
}
}
}
System.out.println(dp[n]);
}
public static boolean IsPrime(int n) {
if(n==1) {
return false;
}
for(int i=2;i<=Math.sqrt(n);i++) {
if(n%i==0) {
return false;
}
}
return true;
}
}10. 求最大值
给n个有序整数对ai bi,你需要选择一些整数对 使得所有你选定的数的ai+bi的和最大。并且要求你选定的数对的ai之和非负,bi之和非负。
输入格式
输入的第一行为n,数对的个数。以下n行每行两个整数 ai bi
输出格式
输出你选定的数对的ai+bi之和
样例输入
5
-403 -625
-847 901
-624 -708
-293 413
886 709
样例输出
1715
数据规模和约定
1<=n<=100。-1000<=ai,bi<=1000
代码:
import java.util.*;
/*
* dp[i][j] 前i个数对中,选的a和为j时,b和最大值
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = 100000;
int max = 200000;
int n = sc.nextInt();
int[] a = new int[n+1];
int[] b = new int[n+1];
int[][] dp = new int[n+1][max+1];
for(int i=1;i<=n;i++) {
a[i] = sc.nextInt();
b[i] = sc.nextInt();
}
for(int i=0;i<=n;i++) {
Arrays.fill(dp[i], -0x3f3f3f);
}
//a有可能是负,下标不能为负,所以加上偏移量t
for(int i=1;i<=n;i++) {
dp[i][t+a[i]] = b[i];
}
for(int i=1;i<=n;i++) {
for(int j=0;j<=max;j++) {
//不使用a[i]使a的和为j
dp[i][j] = Math.max(dp[i][j], dp[i-1][j]);
//判断是否越界
if(j-a[i]>=0 && j-a[i]<=max) {
//使用a[i]使a的和为j
dp[i][j] = Math.max(dp[i][j], dp[i-1][j-a[i]]+b[i]);
}
}
}
int res = 0;
//从t开始,保证a的和为正
for(int i=t;i<=max;i++) {
//b的和非负
if(dp[n][i] >=0) {
//b的和加上a的和减去偏移量t
res = Math.max(res, dp[n][i]+i-t);
}
}
System.out.println(res);
}
}11. 概率计算
生成n个∈[a,b]的随机整数,输出它们的和为x的概率。
输入格式
一行输入四个整数依次为n,a,b,x,用空格分隔。
输出格式
输出一行包含一个小数位和为x的概率,小数点后保留四位小数
样例输入
2 1 3 4
样例输出
0.3333
数据规模和约定
对于50%的数据,n≤5。对于100%的数据,n≤100,b≤100。
代码:
import java.util.*;
/*
* dp[i][j] 前i个整数中和等于j的概率
* 假设第i个数为k,则i个数和为j的情况等价于前i-1个数和为j-k的概率乘以k的概率,即:
* dp[i][j] = dp[i-1][j-k]*1.0/(b-a+1)
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int a = sc.nextInt();
int b = sc.nextInt();
int x = sc.nextInt();
double[][] dp = new double[n+1][n*b+1];
for(int i=a;i<=b;i++) {
dp[1][i] = 1.0/(b-a+1);
}
for(int i=2;i<=n;i++) {
//k是[a,b]之间的数
for(int k=a;k<=b;k++) {
for(int j=1;j<=x;j++) {
if(j>k) {
dp[i][j] += dp[i-1][j-k]*1.0/(b-a+1);
}
}
}
}
System.out.printf("%.4f", dp[n][x]);
}
}12. 印章
共有n种图案的印章,每种图案的出现概率相同。小A买了m张印章,求小A集齐n种印章的概率。
输入格式
一行两个正整数n和m
输出格式
一个实数P表示答案,保留4位小数。
样例输入
2 3
样例输出
0.7500
数据规模和约定
1≤n,m≤20
代码:
import java.util.*;
/*
* dp[i][j] i张印章j种印章的概率
* 1.如果i<j,则集齐的概率为0
* 2.如果i==j&&j==1,即i和j相等且印章重复为同一种,概率为 n*pow(1/n,i) = pow(1/n,i-1);
* 3.如果i>j&&j!=1,分两种情况:
* 3.1 第i张的种类之前已经出现过,概率为dp[i-1][j]*j*1.0/n
* 3.2 第i张的种类是新的,以前没有出现过,概率为dp[i-1][j-1]*(n-(j-1))*1.0/n
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
double[][] dp = new double[m+1][n+1];
for(int i=1;i<=m;i++) {
for(int j=1;j<=n;j++) {
if(i<j) {
dp[i][j] = 0;
}
if(i==j && j==1) {
dp[i][j] = Math.pow(1.0/n,i-1);
}
else {
dp[i][j] = dp[i-1][j]*j*1.0/n + dp[i-1][j-1]*(n-(j-1))*1.0/n;
}
}
}
System.out.printf("%.4f",dp[m][n]);
}
}13. 最短Hamilton路径(状态压缩)
给定一张n个点的带权无向图,点从 0∼n−1标号,求起点0到终点 n−1的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数n。
接下来n行每行n个整数,其中第i行第j个整数表示点i到j的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x],并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤107
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18
讲解视频:AcWing 91. 最短Hamilton路径 - AcWing
代码:
import java.util.*;
/*
f[state][j] = f[state_k][k] + w[k][j], state_k代表除去j之后合集,state_k要包含k
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] w = new int[n][n];
int[][] f = new int[1<<n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
w[i][j] = sc.nextInt();
}
}
for(int i=0;i< 1<<n;i++) {
Arrays.fill(f[i], Integer.MAX_VALUE>>1);
}
f[1][0] = 0;
for(int i=0;i < 1<<n;i++){
for(int j=0;j<n;j++){
//第i状态下j是不是1,看状态是否合法(是否包含j)
if((i>>j & 1)==1){
for(int k=0;k<n;k++){
if((i >> k & 1)==1){
f[i][j] = Math.min(f[i][j], f[i-(1<<j)][k]+w[k][j]);
}
}
}
}
}
System.out.println(f[(1<<n) - 1][n-1]);
}
}14. 遍历(状态压缩)
问题描述
给定两张N个点的图,要求找出图中经过指定M个点的一条路径,希望路径最短。
输入格式
第一行两个整数N,M。之后n行每行n个整数,其中第i行的第j个整数x表示i到j的路的长度(i,j从0到n-1)。0表示两点之间没有路。之后一行M个整数,表示指定的点的编号,编号从0开始。
输出格式
一行一个整数表示路径长度。无解输出-1。
样例输入
3 2
0 1 2
3 0 4
5 6 0
0 1
样例输出
1
数据规模和约定
N <= 100 M <= 15
代码:
/*
采用Floyd求每个点之间最短路径,采用3.最短Hamilton路径中路径压缩的思想。
*/
import java.util.*;
public class Main {
static int[][] w;//两点直接的距离
static int n,m;
static int[] q;
static int[][] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
w = new int[n][n];
q = new int[m];
f = new int[1<<m][n];
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
w[i][j] = sc.nextInt();
if(i!=j && w[i][j]==0) {
//MAX_VALUE右移1位为了防止后续相加越位
w[i][j] = Integer.MAX_VALUE>>1;
}
}
}
for(int i=0;i<m;i++) {
q[i] = sc.nextInt();
}
Floyd();
for(int i=0;i < 1<<m;i++) {
Arrays.fill(f[i], Integer.MAX_VALUE>>1);
}
for(int i=0;i<m;i++) {
f[1<<i][i] = 0;
}
for(int i=0;i<1<<m;i++) {
for(int j=0;j<m;j++) {
if((i>>j & 1)==1) {
for(int k=0;k<m;k++) {
if((i>>k & 1) ==1) {
f[i][j] = Math.min(f[i][j], f[i-(1<<j)][k]+w[q[k]][q[j]]);
}
}
}
}
}
int min = Integer.MAX_VALUE;
for(int i=0;i<m;i++) {
min = Math.min(min, f[(1<<m)-1][i]);
}
if(min == Integer.MAX_VALUE) {
System.out.print(-1);
}
else {
System.out.println(min);
}
}
//计算两点之间最短路径
public static void Floyd() {
for(int k=0;k<n;k++) {
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
w[i][j] = Math.min(w[i][j], w[i][k]+w[k][j]);
}
}
}
}
}数位DP
数位DP学习整理(数位DP看完这篇你就会了)_unique_pursuit的博客-CSDN博客
15. 二进制问题(数位dp)
小蓝最近在学习二进制。他想知道 1 到 N 中有多少个数满足其二进制表示中恰好有 K 个 1。你能帮助他吗?
输入描述
输入一行包含两个整数 N 和 K。
输出描述
输出一个整数表示答案。
输入样例
7 2
输出样例
3
评测用例规模与约定
对于 30% 的评测用例,1≤N≤106,1≤K≤10。
对于 60% 的评测用例,1≤N≤2×109,1≤K≤30。
对于所有评测用例,1≤N≤1018,1≤K≤50。
代码:
import java.util.*;
public class Main {
static long n;
static int k;
static long[][] dp = new long[66][66];
static String string;
static int[] num = new int[66];
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextLong();
k = sc.nextInt();
for (int i = 0; i < dp.length; i++) {
Arrays.fill(dp[i], -1);
}
System.out.println(solve(n));
}
/*
* 当前取的位长度,已有1的个数,limit判断前面的位是否按照边界n来取的
* 如:n的二进制是1001.... , 当前是1000....则后边的数位都比n小,0或者1可以随便取,limit一直false
*/
public static long dfs(int len, int sum, boolean limit) {
//1的数量等于k,则符合题意返回1,加1
if (len == 0) {
return sum == k ? 1 : 0;
}
//如果当前状态处理过并且对后边取位没有影响
if (dp[len][sum] != -1 && !limit) {
return dp[len][sum];
}
//如果前面按照n边界取,最大可取n对应的位的数
int up;
if (limit) {
up = num[len];
}
//没有影响,可以随便取,最大取1
else {
up = 1;
}
long res = 0;
for (int i = 0; i <= up; i++) {
if (i == 1) {
res += dfs(len-1, sum+1, limit && i == up);
}
else {
res += dfs(len-1, sum, limit && i == up);
}
}
return dp[len][sum] = res;
}
public static long solve(long n) {
int len = 0;
//转为倒序二进制
while (n != 0) {
num[++len] = (int)(n & 1);
n >>= 1;
}
return dfs(len, 0, true);
}
}并查集
1.修改数组
给定一个长度为 N 的数组 A = [A1, A2, · · · AN ],数组中有可能有重复出现 的整数。现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A2,A3,··· ,AN。当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则 小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直 到 Ai 没有在 A1 ∼ Ai−1 中出现过。当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。 现在给定初始的 A 数组,请你计算出最终的 A 数组。
输入描述
第一行包含一个整数 N。 第二行包含N个整数A1,A2,··· ,AN
输出描述
输出N个整数,依次是最终的A1,A2,··· ,AN。
样例输入
5
2 1 1 3 4
样例输出
2 1 3 4 5
代码:
import java.util.*;
public class Main {
static int[] f = new int[2000000];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
for (int i = 1; i < f.length; i++) {
f[i] = i;
}
int n = sc.nextInt();
int[] arr = new int[n+1];
for (int i = 1; i <= n; i++) {
arr[i] = sc.nextInt();
}
for (int i = 1; i <= n; i++) {
//查找该点的父亲
int fa = find(arr[i]);
//该点等于父亲
arr[i] = fa;
//父亲变为新节点+1
f[fa] = find(fa+1);
}
for (int i = 1; i <= n ; i++) {
System.out.print(arr[i]+" ");
}
}
//并查集
public static int find(int x) {
if (f[x] != x) {
f[x] = find(f[x]);
}
return f[x];
}
}贪心算法
1.防御力
小明最近在玩一款游戏。对游戏中的防御力很感兴趣。我们认为直接影响防御的参数为“防御性能”,记作d,而面板上有两个防御值A和B,与d成对数关系,(注意任何时候上式都成立)。在游戏过程中,可能有一些道具把防御值A增加一个值,有另一些道具把防御值B增加一个值。现在小明身上有n1个道具增加A的值和n2个道具增加B的值,增加量已知。现在已知第i次使用的道具是增加A还是增加B的值,但具体使用那个道具是不确定的,请找到一个字典序最小的使用道具的方式,使得最终的防御性能最大。初始时防御性能为0,即d=0,所以A=B=1。
输入描述
输入的第一行包含两个数n1,n2,空格分隔。第二行n1个数,表示增加A值的那些道具的增加量。
第三行n2个数,表示增加B值的那些道具的增加量。第四行一个长度为n1+n2的字符串,由0和1组成,表示道具的使用顺序。0表示使用增加A值的道具,1表示使用增加B值的道具。输入数据保证恰好有n1个0,n2个1。
输出格式
对于每组数据,输出n1+n2+1行,前n1+n2行按顺序输出道具的使用情况,若使用增加A值的道具,输出Ax,x为道具在该类道具中的编号(从1开始)。若使用增加B值的道具则输出Bx。最后一行输出一个大写字母E。
样例输入
1 2
4
2 8
101
样例输出
B2
A1
B1
E
样例说明
操作 d A B
初始 0 1 1
B2 2 4 9
A1 3 8 27
B1 log3(29) 2^(log3(29)) 29
代码:
import java.util.*;
/*
* A按照升序,B按照降序时,最后的结果最大
*/
public class Main1 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n1 = sc.nextInt();
int n2 = sc.nextInt();
int[] a = new int[n1+1];
int[] b = new int[n2+1];
//list存储A和B的下标
ArrayList<Integer> list1 = new ArrayList<Integer>();
ArrayList<Integer> list2 = new ArrayList<Integer>();
for (int i = 1; i <= n1; i++) {
a[i] = sc.nextInt();
list1.add(a[i]);
}
for (int i = 1; i <= n2; i++) {
b[i] = sc.nextInt();
list2.add(b[i]);
}
String string = sc.next();
Arrays.sort(a);
Arrays.sort(b);
int index1 = 1, index2 = n2;
for (int i = 0; i < string.length(); i++) {
//A升序
if (string.charAt(i) == '0') {
System.out.print("A");
System.out.println(list1.indexOf(a[index1++])+1);
}
//B降序
if (string.charAt(i) == '1') {
System.out.print("B");
System.out.println(list2.indexOf(b[index2--])+1);
}
}
System.out.println("E");
}
}2.排座椅
上课的时候总有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的D对同学上课时会交头接耳。同学们在教室中坐成了M行N列,坐在第i行第j列的同学的位置是(i,j),为了方便同学们进出,在教室中设置了K条横向的通道,L条纵向的通道。于是,聪明的小雪想到了一个办法,或许可以减少上课时学生交头接耳的问题:她打算重新摆放桌椅,改变同学们桌椅间通道的位置,因为如果一条通道隔开了两个会交头接耳的同学,那么他们就不会交头接耳了。请你帮忙给小雪编写一个程序,给出最好的通道划分方案。在该方案下,上课时交头接耳的学生对数最少。
输入描述
输入第一行,有5各用空格隔开的整数,分别是M,N,K,L,D(2<=N,M<=1000,0<=K<M,0<=L<N,D<=2000)。下来D行,每行有4个用空格隔开的整数,第i行的4个整数Xi,Yi,Pi,Qi,表示坐在位置(Xi,Yi)与(Pi,Qi)的两个同学会交头接耳(输入保证他们前后相邻或者左右相邻)。输入数据保证最优方案的唯一性。
输出描述
第一行包含K个整数,a[1] a[2] … a[K],表示第a[1]行和a[1+1]行之间、第a[2]行和第a[2+1]行之间、…、第a[K]行和第a[K+1]行之间要开辟通道,其中a[i]< a[i+1],每两个整数之间用空格隔开(行尾没有空格)。第二行包含L个整数,b[1] b[2] … b[k],表示第b[1]列和b[1+1]列之间、第b[2]列和第b[2+1]列之间、…、第b[L]列和第b[L+1]列之间要开辟通道,其中b[i]< b[i+1],每两个整数之间用空格隔开(行尾没有空格)。
输入样例
4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4
输出样例
2
2 4
代码:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt();
int n = sc.nextInt();
int k = sc.nextInt();
int l = sc.nextInt();
int d = sc.nextInt();
//记录位置和出现的次数
int[] cnt1 = new int[m];
int[] cnt2 = new int[n];
for (int i = 0; i < d; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int p = sc.nextInt();
int q = sc.nextInt();
//在同一行,进行竖向隔离
if (x == p) {
int index = Math.min(y, q);
cnt2[index]++;
}
//在同一列,进行横向隔离
else if (y == q) {
int index = Math.min(x, p);
cnt1[index]++;
}
}
//尽可能多的使用横向通道将学生隔开,将cnt1中前k大的下标输出
ArrayList<Integer> list1 = new ArrayList<Integer>();
//查找前k大的数的下标存进list
for (int i = 0; i < k; i++) {
int max = -1, index = -1;
for (int j = 0; j < cnt1.length; j++) {
if (max < cnt1[j]) {
max = cnt1[j];
index = j;
}
}
//将最大的设为0,方便查找除它外最大的
cnt1[index] = 0;
list1.add(index);
}
//尽可能多的使用竖向通道将学生隔开,将cnt2中前l大的下标输出
ArrayList<Integer> list2 = new ArrayList<Integer>();
//查找前l大的数的下标存进list
for (int i = 0; i < l; i++) {
int max = -1, index = -1;
for (int j = 0; j < cnt2.length; j++) {
if (max < cnt2[j]) {
max = cnt2[j];
index = j;
}
}
//将最大的设为0,方便查找除它外最大的
cnt2[index] = 0;
list2.add(index);
}
//将list中序号进行排序输出
list1.sort(null);
list2.sort(null);
for (int i = 0; i < list1.size(); i++) {
System.out.print(list1.get(i)+" ");
}
System.out.println();
for (int i = 0; i < list2.size(); i++) {
System.out.print(list2.get(i)+" ");
}
}
}
3.付账问题
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。现在有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 ai 元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?为了公平起见,我们希望在总付钱量恰好为 S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 分钱的整数倍。你需要输出最小的标准差是多少。标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的“偏差有多大”。形式化地说,设第 i 个人付的钱为 bi 元,那么标准差为 :
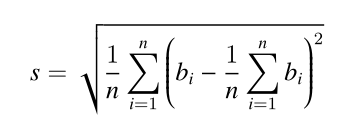
输入格式
第一行包含两个整数 n、S;第二行包含 n 个非负整数 a1, …, an。
输出格式
输出最小的标准差,四舍五入保留 4 位小数。
数据范围
1≤n≤5×105,
0≤ai,S≤109
输入样例1:
5 2333
666 666 666 666 666
输出样例1:
0.0000
输入样例2:
10 30
2 1 4 7 4 8 3 6 4 7
1
2
输出样例2:
0.7928
代码:
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
String[] strings = bf.readLine().split(" ");
int n = Integer.parseInt(strings[0]);
long s = Long.parseLong(strings[1]);
long[] arr = new long[n];
String[] data = bf.readLine().split(" ");
//每个人带的钱数
for (int i = 0; i < arr.length; i++) {
arr[i] = Long.parseLong(data[i]);
}
double avg = 1.0*s/n;
double sum = 0;
Arrays.sort(arr);
for (int i = 0; i < n; i++) {
//钱数少于平均值,将自己的钱全部拿出
if (arr[i]*(n-i) < s) {
sum += Math.pow(arr[i]-avg, 2);
//更新剩余的总金额
s -= arr[i];
}
//多于平均值,后边的都会多于平均值
else {
double cur_avg = 1.0*s/(n-i);
sum += Math.pow(cur_avg-avg, 2)*(n-i);
break;
}
}
System.out.printf("%.4f", Math.sqrt(sum/n));
}
}4.旅行家的预算
一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市(假设出发时油箱是空的)。给定两个城市之间的距离 D1、汽车油箱的容量 C(以升为单位)、每升汽油能行驶的距离 D2、出发点每升汽油价格P 和沿途油站数N(N 可以为零),油站 i 离出发点的距离Di、每升汽油价格 Pi(i=1,2,⋯N)。计算结果四舍五入至小数点后两位。如果无法到达目的地,则输出 No Solution。
输入描述
第一行,D1,C,D2,P,N。接下来有 N 行。第i+1 行,两个数字,油站i 离发点的距离 Di 和每升汽油价格Pi。
输出描述
输出所需最小费用,计算结果四舍五入至小数点后两位。如果无法到达目的地,则输出 No Solution。
样例输入
275.6 11.9 27.4 2.8 2
102.0 2.9
220.0 2.2
样例输出
26.95
代码:
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
double d1 = sc.nextDouble();
double c = sc.nextDouble();
double d2 = sc.nextDouble();
double p = sc.nextDouble();
int n = sc.nextInt();
//起点+n个加油站+终点
double[] distance = new double[n+2];
double[] price = new double[n+2];
for (int i = 1; i <= n; i++) {
distance[i] = sc.nextDouble();
price[i] = sc.nextDouble();
}
//起点
distance[0] = 0;
price[0] = p;
//终点
distance[n+1] = d1;
price[n+1] = 0;
//如果两加油站需要的油量比油箱总量大,无解
for (int i = 0; i <= n; i++) {
if (distance[i+1]-distance[i] > c*d2) {
System.out.println("No Solution");
return;
}
}
double perMaxDis = c*d2;
double Allprices = 0;
double curOil = 0;
//当前加油站
int i = 0;
while (i <= n){
//可选择的加油站
int j = 0;
//查找能到达的价格低的加油站
for (j = i+1; j <= n+1; j++) {
//到达不了j加油站,只能到上一个
if (distance[j]-distance[i] > perMaxDis) {
j--;
break;
}
//下一个比当前的油价便宜的加油站
if (price[j] <= price[i]) {
break;
}
}
//能到比当前便宜的加油站,只需使油量恰好到下一便宜的加油站
if (price[j] <= price[i]) {
Allprices += price[i]*((distance[j]-distance[i])/d2-curOil);
curOil = 0;
}
//到不了下一个便宜的加油站即当前是最便宜的,加满
else {
Allprices += (c-curOil)*price[i];
//开完后剩余的油
curOil = c-(distance[j]-distance[i])/d2;
}
//从i开到j
i = j;
}
System.out.printf("%.2f", Allprices);
}
}5.巧克力
小蓝很喜欢吃巧克力,他每天都要吃一块巧克力。一天小蓝到超市想买一些巧克力。超市的货架上有很多种巧克力,每种巧克力有自己的价格、数量和剩余的保质期天数,小蓝只吃没过保质期的巧克力,请问小蓝最少花多少钱能买到让自己吃 x 天的巧克力。
输入描述
输入的第一行包含两个整数x,n,分别表示需要吃巧克力的天数和巧克力的种类数。接下来 n 行描述货架上的巧克力,其中第 i 行包含三个整数ai,bi,ci,表示第 i 种巧克力的单价为 ai,保质期还剩 bi 天(从现在开始的 bi 天可以吃),数量为 ci。
输出描述
输出一个整数表示小蓝的最小花费。如果不存在让小蓝吃 x 天的购买方案,输出 −1。
输入样例
10 3
1 6 5
2 7 3
3 10 10
输出样例
18
样例说明
一种最佳的方案是第 1 种买 5 块,第 2 种买 2 块,第 3 种买 3 块。前 5天吃第 1 种,第 6、7 天吃第 2 种,第 8 至 10 天吃第 3 种。
评测用例规模与约定
对于 30% 的评测用例,n,x≤1000;
对于所有评测用例,1≤n,x≤100000,1≤ai,bi,ci≤1000000000。
代码:
import java.util.*;
public class Main {
public static class Chocolate{
int price,day,num;
public Chocolate(int price, int day, int num) {
this.price = price;
this.day = day;
this.num = num;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt();
int n = sc.nextInt();
ArrayList<Chocolate> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
list.add(new Chocolate(a, b, c));
}
list.sort(new Comparator<Chocolate>() {
public int compare(Chocolate chocolate1, Chocolate chocolate2){
//若价格相等,则按保质期排序,否则按价格排序
if (chocolate1.price == chocolate2.price) {
if (chocolate1.day == chocolate2.day) {
return chocolate1.num - chocolate2.num;
}
return chocolate1.day - chocolate2.day;
}
return chocolate1.price - chocolate2.price;
}
});
int needs = x;
long money = 0;
//从后往前一块一块的买
while (needs > 0) {
int i = 0;
while (i < n) {
int price = list.get(i).price;
int day = list.get(i).day;
int num = list.get(i).num;
//如果保质期可以满足,并且还有剩余
if (day >= needs && num > 0) {
list.get(i).num--;
money += price;
break;
}
i++;
}
//所有的巧克力都不满足,无解
if (i == n) {
System.out.println(-1);
return;
}
needs--;
}
System.out.println(money);
}
}二分查找
1. 123
小蓝发现了一个有趣的数列,这个数列的前几项如下:1, 1, 2, 1, 2, 3, 1, 2, 3, 4, ...
小蓝发现,这个数列前 1 项是整数 1,接下来 2 项是整数 1 至 2,接下来3 项是整数 1 至 3,接下来 4 项是整数 1 至 4,依次类推。小蓝想知道,这个数列中,连续一段的和是多少?
输入格式
输入的第一行包含一个整数 T,表示询问的个数。
接下来 T 行,每行包含一组询问,其中第 i 行包含两个整数 li 和 ri,表示询问数列中第 li 个数到第 ri 个数的和。
输出格式
输出 T 行,每行包含一个整数表示对应询问的答案。
样例输入
3
1 1
1 3
5 8
样例输出
1
4
8
评测用例规模与约定
对于 10% 的评测用例, 1 ≤ T ≤ 30, 1 ≤ li ≤ ri ≤ 100。
对于 20% 的评测用例, 1 ≤ T ≤ 100, 1 ≤ li ≤ ri ≤ 1000。
对于 40% 的评测用例, 1 ≤ T ≤ 1000, 1 ≤ li ≤ ri ≤ 10 ^ 6。
对于 70% 的评测用例, 1 ≤ T ≤ 10000, 1 ≤ li ≤ ri ≤ 10 ^ 9。
对于 80% 的评测用例, 1 ≤ T ≤ 1000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
对于 90% 的评测用例, 1 ≤ T ≤ 10000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
对于所有评测用例, 1 ≤ T ≤ 100000, 1 ≤ li ≤ ri ≤ 10 ^ 12。
代码:
import java.util.*;
/* index sum num
* 1 1 1 1
* 2 1 2 4 3
* 3 1 2 3 10 6
* 4 1 2 3 4 20 10
* 5 1 2 3 4 5 35 15
* n 1 2 ... n
*
* num[i] = num[i-1] + i;
* sum[i] = sum[i-1] + num[i]
* 对于数列中任意位置 i ,一定存在一个最大的 j 满足 num[j]≤i ,这表示第 i 个数落在第 j+1 区间内
* 对于数列中任意位置i,当它落在第 j+1 个区间,它是该区间第 k 个数,则它在数列中的前缀和为:sum[j]+num[k],其中 k=i−num[j]。
*/
public class Main {
static int maxn = 1414215;
static long[] sum,num;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sum = new long[maxn];
num = new long[maxn];
for (int i = 1; i < maxn; i++) {
num[i] = num[i-1] + i;
sum[i] = sum[i-1] + num[i];
}
for (int i = 0; i < n; i++) {
long start = sc.nextLong();
long end = sc.nextLong();
System.out.println(preSum(end)-preSum(start-1));
}
}
public static long preSum(long i) {
int l = 0, r = maxn, mid;
//二分查找
while(l <= r) {
mid = (l+r)/2;
if (num[mid] > i) {
r = mid - 1;
}
else {
l = mid + 1;
}
}
l--;
return sum[l] + num[(int) (i-num[l])];
}
}2.跳石头
一年一度的“跳石头”比赛又要开始了!这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终 点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达 终点。为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳 跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能 移走起点和终点的岩石)。
输入描述:
输入文件第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终 点之间的岩石数,以及组委会至多移走的岩石数。接下来 N 行,每行一个整数,第 i 行的整数 Di(0 < Di < L)表示第 i 块岩石与 起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同 一个位置。
输出格式:
输出只包含一个整数,即最短跳跃距离的最大值。
输入样例:
25 5 2
2
11
14
17
21
输出样例:
4
说明
输入输出样例 1 说明:将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
另:对于 20%的数据,0 ≤ M ≤ N ≤ 10。 对于50%的数据,0 ≤ M ≤ N ≤ 100。对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
代码:
import java.util.*;
public class Main {
static int[] arr;
static int m;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int l = sc.nextInt();
int n = sc.nextInt();
m = sc.nextInt();
arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
//二分查找最合适的距离
int left = 0, right = l, mid, res = 0;
while (left <= right) {
mid = (left + right)/2;
//可以满足,继续查找看有没有更大的
if (check(mid)) {
res = mid;
left = mid +1;
}
//不能满足,说明距离太大了
else {
right = mid - 1;
}
}
System.out.println(res);
}
public static boolean check(int d) {
//cnt记录搬走石头块数,pos为当前的石头到起点的距离
int cnt = 0, pos = 0;
for (int i = 0; i < arr.length; i++) {
//从起跳的石头到第i个石头的距离比d小,则可以搬走
if (arr[i] - pos < d) {
cnt++;
}
//从起跳的石头到第i个石头的距离>=d,则不可以搬走,需要跳到该石头
else {
pos = arr[i];
}
}
//搬走的石头数大于m,则距离d不满足
if (cnt > m) {
return false;
}
else {
return true;
}
}
}输入输出
几种常用的输入输出方式。
1:Scanner 类最慢,但是最好用,因为这个类没有缓存处理,所以io方面大量输入读取特别慢。
Scanner sc=new Scanner(System.in);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); 2:bufferedreader类最不方便,但是可以满足大部分输入速度的需求,输入缺点就是只能按行读取数据,必要时需要字符串分割,转成int以及其他类型还需要转换。这种输入方式只能输入字符串然后分割处理等等,效率比Scanner高很多
BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out)); 3:StreamTokenizer类最快,他的底层是用字符分割,但是这样处理有很大局限性。输入string类型除了纯字母。否则混合输入会出错,特殊符号在字符串中输入也不行。
StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
in.nextToken();int n=(int)in.nval;
in.nextToken();long p=(long)in.nval;
in.nextToken();double q=in.nval;
out.print(n);
out.flush();图论

1.发现环(拓扑排序)
小明的实验室有N 台电脑,编号1⋯N。原本这N 台电脑之间有N−1 条数据链接相连,恰好构成一个树形网络。在树形网络上,任意两台电脑之间有唯一的路径相连。不过在最近一次维护网络时,管理员误操作使得某两台电脑之间增加了一条数据链接,于是网络中出现了环路。环路上的电脑由于两两之间不再是只有一条路径,使得这些电脑上的数据传输出现了 BUG。为了恢复正常传输。小明需要找到所有在环路上的电脑,你能帮助他吗?
输入描述
输入范围:第一行包含一个整数N 。以下N 行每行两个整数 a,b,表示a 和 b 之间有一条数据链接相连。其中,1≤N≤105,1≤a,b≤N。输入保证合法。
输出描述
按从小到大的顺序输出在环路上的电脑的编号,中间由一个空格分隔。
输入样例
5
1 2
3 1
2 4
2 5
5 3
输出样例
1 2 3 5
代码:
import java.io.*;
import java.util.*;
public class Main {
//存放相连的点都有哪些点
static ArrayList<Integer>[] edges;
//存放节点的入度
static int[] in;
//存放入度不为1的点
static ArrayList<Integer> list = new ArrayList<Integer>();
//队列用于拓扑排序
static Queue<Integer> queue = new LinkedList<Integer>();
public static void main(String[] args) throws IOException {
StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
st.nextToken();
int n = (int)st.nval;
in = new int[n+1];
edges = new ArrayList[n+1];
for (int i = 1; i <= n; i++) {
edges[i] = new ArrayList<Integer>();
}
for (int i = 1; i <= n; i++) {
st.nextToken();
int a = (int) st.nval;
st.nextToken();
int b = (int) st.nval;
//a,b两点相连
edges[a].add(b);
edges[b].add(a);
//两个点入度分别加一
in[a]++;
in[b]++;
}
//拓扑排序,将入度为1的点去掉,添加到队列
for (int i = 1; i <= n; i++) {
if (in[i] == 1) {
queue.add(i);
}
}
while (!queue.isEmpty()) {
int node = queue.poll();
//将node点去掉,把与node相连的点入度都减1
for (int i : edges[node]) {
in[i]--;
if (in[i] == 1) {
queue.add(i);
}
}
}
for (int i = 1; i < in.length; i++) {
//该点入度不为1,则在环中
if (in[i] > 1) {
list.add(i);
}
}
list.sort(null);
for (int i : list) {
pw.print(i+" ");
}
pw.flush();
}
}2. 出差(Dijkstra最短路径)
A 国有 N 个城市,编号为 1 . . . N。小明是编号为 1 的城市中一家公司的员工,今天突然接到了上级通知需要去编号为 N 的城市出差。由于疫情原因,很多直达的交通方式暂时关闭,小明无法乘坐飞机直接从城市 1 到达城市 N,需要通过其他城市进行陆路交通中转。小明通过交通信息网,查询到了 M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。同样由于疫情原因,小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络,小明也查询到了各个城市的隔离信息。(由于小明之前在城市 1,因此可以直接离开城市 1,不需要隔离)。由于上级要求,小明希望能够尽快赶到城市 N,因此他求助于你,希望你能帮他规划一条路线,能够在最短时间内到达城市 N。
输入格式
第 1 行:两个正整数 N, M,N 表示 A 国的城市数量,M 表示未关闭的路线数量
第 2 行:N 个正整数,第 i 个整数 Ci 表示到达编号为 i 的城市后需要隔离的时间
第 3 . . . M + 2 行:每行 3 个正整数,u, v, c,表示有一条城市 u 到城市 v 的双向路线仍然开通着,通过该路线的时间为 c
输出格式
第 1 行:1 个正整数,表示小明从城市 1 出发到达城市 N 的最短时间(到达城市 N,不需要计算城市 N 的隔离时间)
样例输入
4 4
5 7 3 4
1 2 4
1 3 5
2 4 3
3 4 5
样例输出
13
代码:
import java.util.*;
public class Main {
//城市之间的时间
static int[][] distance;
//quarantine记录隔离时间
static int[] quarantine;
//记录从某城市出发的最早时间
static int[] dp;
static boolean[] visit;
static int n;
static int MAXN = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int m = sc.nextInt();
distance = new int[n+1][n+1];
quarantine = new int[n+1];
dp = new int[n+1];
for (int i = 1; i <= n; i++) {
quarantine[i] = sc.nextInt();
}
//初始化邻接矩阵
for (int i = 1; i <= n; i++) {
Arrays.fill(distance[i], MAXN);
distance[i][i] = 0;
}
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int dis = sc.nextInt();
distance[a][b] = distance[b][a] = dis;
}
visit = new boolean[n+1];
dijkstra();
System.out.println(dp[n]-quarantine[n]);
}
public static void dijkstra() {
Arrays.fill(dp, MAXN);
dp[1] = 0;
for (int iter = 0; iter < n; iter++) {
//每次找到【最短距离最小】 且【未被更新】的点t
int t = -1;
for (int i = 1; i <= n; i++) {
if (!visit[i] && (t == -1 || dp[i] < dp[t])) {
t = i;
}
}
visit[t] = true;
//使用t的最小距离更新其他点
for (int i = 1; i <= n; i++) {
dp[i] = Math.min(dp[i], dp[t]+distance[t][i]+quarantine[i]);
}
}
}
}3.治理环境(floyd最短路径+二分查找)
LQ 国拥有 n 个城市,从 0 到 n − 1 编号,这 n 个城市两两之间都有且仅有一条双向道路连接,这意味着任意两个城市之间都是可达的。每条道路都有一个属性 D ,表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时,可能存在多条路线,每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和,LQ 国的人都很讨厌灰尘,所以他们总会优先选择灰尘度最小的路线。
LQ 国很看重居民的出行环境,他们用一个指标 P 来衡量 LQ 国的出行环境,P 定义为:
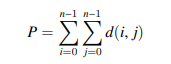
其中 d(i, j) 表示城市 i 到城市 j 之间灰尘度最小的路线对应的灰尘度的值。为了改善出行环境,每个城市都要有所作为,当某个城市进行道路改善时,会将与这个城市直接相连的所有道路的灰尘度都减少 1,但每条道路都有一个灰尘度的下限值 L,当灰尘度达到道路的下限值时,无论再怎么改善,道路的灰尘度也不会再减小了。具体的计划是这样的:
第 1 天,0 号城市对与其直接相连的道路环境进行改善;
第 2 天,1 号城市对与其直接相连的道路环境进行改善;
…
第 n 天,n − 1 号城市对与其直接相连的道路环境进行改善;
第 n + 1 天,0 号城市对与其直接相连的道路环境进行改善;
第 n + 2 天,1 号城市对与其直接相连的道路环境进行改善;
…
LQ 国想要使得 P 指标满足 P ≤ Q。请问最少要经过多少天之后,P 指标可以满足 P ≤ Q。如果在初始时就已经满足条件,则输出 0 ;如果永远不可能满足,则输出 −1。
输入格式
输入的第一行包含两个整数 n, Q,用一个空格分隔,分别表示城市个数和期望达到的 P 指标。接下来 n 行,每行包含 n 个整数,相邻两个整数之间用一个空格分隔,其中第 i 行第 j 列的值 Dij (Dij = Dji, Dii = 0) 表示城市 i 与城市 j 之间直接相连的那条道路的灰尘度。接下来 n 行,每行包含 n 个整数,相邻两个整数之间用一个空格分隔,其中第 i 行第 j 列的值 Lij (Lij = Lji, Lii = 0) 表示城市 i 与城市 j 之间直接相连的那条道路的灰尘度的下限值。
输出格式
输出一行包含一个整数表示答案。
样例输入
3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0
样例输出
2
代码:
import java.util.*;
public class Main {
static int n;
static long q;
//分别记录道路的灰尘度和下限
static long[][] w,limit;
//记录两点之间的最小灰尘度
static long[][] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
q = sc.nextLong();
w = new long[n][n];
limit = new long[n][n];
dp = new long[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
w[i][j] = sc.nextLong();
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
limit[i][j] = sc.nextLong();
dp[i][j] = limit[i][j];
}
}
//此时dp最短路径为下限,如果此时比q大,则永远都不可能满足
if (floyd() > q) {
System.out.println(-1);
return;
}
//二分查找符合的天数
long l = 0, r = 10000010;
while (l < r) {
long mid = (l+r)/2;
//p > q,则需要添加天数,继续改善
if (check(mid)) {
l = mid+1;
}
else {
r = mid;
}
}
System.out.println(l);
}
//判断是否当前天数是否符合题意
public static boolean check(long x) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = w[i][j];
}
}
//判断改善了几轮,还余几天
long h = x/n;
long s = x%n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
continue;
}
//因为有下限,所以取较大的值
if (s > i) {
dp[i][j] = Math.max(limit[i][j], dp[i][j]-h-1);
}
else {
dp[i][j] = Math.max(limit[i][j], dp[i][j]-h);
}
dp[j][i] = dp[i][j];
}
}
//改善后使用floyd求P,判断是否符合
return floyd() > q ;
}
//floyd求最短路径,最后返回所有节点最短路径和,即题目中的P
public static long floyd() {
long p = 0;
//从i到j的路径,k为中间节点
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k][j]);
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
p += dp[i][j];
}
}
return p;
}
}4.通电(最小生成树)
2015年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。这一次,小明要帮助 n 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。现在,这 n 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为:
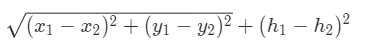
高度的计算方式与横纵坐标的计算方式不同。由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
输入格式
输入的第一行包含一个整数 n ,表示村庄的数量。接下来 n 行,每个三个整数 x, y, h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
输出格式
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
样例输入
4
1 1 3
9 9 7
8 8 6
4 5 4
样例输出
17.41
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 1000,0 <= x, y, h <= 10000。
prim最小生成树代码:
import java.util.*;
public class Main {
static class Node{
double x,y,h;
public Node(double x,double y,double h) {
this.x = x;
this.y = y;
this.h = h;
}
}
static int n;
static Node[] nodes;
static double[][] cost;
//与结点相连的最小边权,即最小花费
static double[] dist;
static boolean[] visit;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
nodes = new Node[n+1];
cost = new double[n+1][n+1];
dist = new double[n+1];
visit = new boolean[n+1];
for (int i = 1; i <= n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
double h = sc.nextDouble();
nodes[i] = new Node(x, y, h);
}
for (int i = 1; i <= n; i++) {
Arrays.fill(cost[i], Double.MAX_VALUE);
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cost[i][j] = cost[j][i] = get(nodes[i], nodes[j]);
}
}
double res = prim();
System.out.printf("%.2f", res);
}
//计算两村庄之间费用
public static double get(Node node1,Node node2) {
double x = node1.x - node2.x;
double y = node1.y - node2.y;
double h = node1.h - node2.h;
return Math.sqrt(x*x+y*y)+h*h;
}
//prim算法求最小生成树
public static double prim() {
Arrays.fill(dist, Double.MAX_VALUE);
dist[1] = 0;
double res = 0;
for (int i = 1; i <= n; i++) {
int t = -1;
//查找未加入最小生成树的结点中距离最小的点
for (int j = 1; j <= n; j++) {
if (!visit[j] && (t == -1 || dist[j] < dist[t])) {
t = j;
}
}
res += dist[t];
visit[t] = true;
//更新未加入结点离最小生成树的距离
for (int j = 1; j <= n; j++) {
if (!visit[j]) {
dist[j] = Math.min(dist[j], cost[t][j]);
}
}
}
return res;
}
}kruskal最小生成树代码:
import java.util.*;
public class Main {
static class Node{
double x,y,h;
public Node(double x,double y,double h) {
this.x = x;
this.y = y;
this.h = h;
}
}
static class Edge{
int x,y;
double cost;
public Edge(int x,int y,double cost) {
this.x = x;
this.y = y;
this.cost = cost;
}
}
static int n;
static Node[] nodes;
static ArrayList<Edge> edges = new ArrayList<>();
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
nodes = new Node[n];
f = new int[n];
for (int i = 0; i < n; i++) {
double x = sc.nextDouble();
double y = sc.nextDouble();
double h = sc.nextDouble();
nodes[i] = new Node(x, y, h);
f[i] = i;
}
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
edges.add(new Edge(i,j,get(nodes[i], nodes[j])));
}
}
kruskal();
}
//计算两村庄之间费用
public static double get(Node node1,Node node2) {
double x = node1.x - node2.x;
double y = node1.y - node2.y;
double h = node1.h - node2.h;
return Math.sqrt(x*x+y*y)+h*h;
}
//kruskal求最小生成树
public static void kruskal() {
double res = 0;
//统计已经连接边的数量,最多有n-1条边相连
int cnt = 0;
//在指定范围内按照花费进行升序排序
edges.sort((o1,o2) -> (int)(o1.cost - o2.cost));
for (int i = 0; i < edges.size(); i++) {
//获取一条边的两个点
Edge edge = edges.get(i);
int x = edge.x;
int y = edge.y;
double cost = edge.cost;
//如果两点没有相同的祖先结点,则代表不是环
if (find(x) != find(y)) {
merge(x, y);
res += cost;
cnt++;
if (cnt == n-1) {
break;
}
}
}
System.out.printf("%.2f", res);
}
//查找x的祖先结点
public static int find(int x) {
if (f[x] != x) {
f[x] = find(f[x]);
}
return f[x];
}
//合并两个结点
public static void merge(int x,int y) {
int px = find(x);
int py = find(y);
f[py] = px;
}
}其他
1.约瑟夫环(链表)
设有 n 个人围坐在圆桌周围,现从某个位置 k 上的人开始报数,报数到 m 的人就站出来。下一个人,即原来的第 m+1 个位置上的人,又从 1 开始报数,再报数到 m 的人站出来。依次重复下去,直到全部的人都站出来为止。试设计一个程序求出这 n 个人的出列顺序。
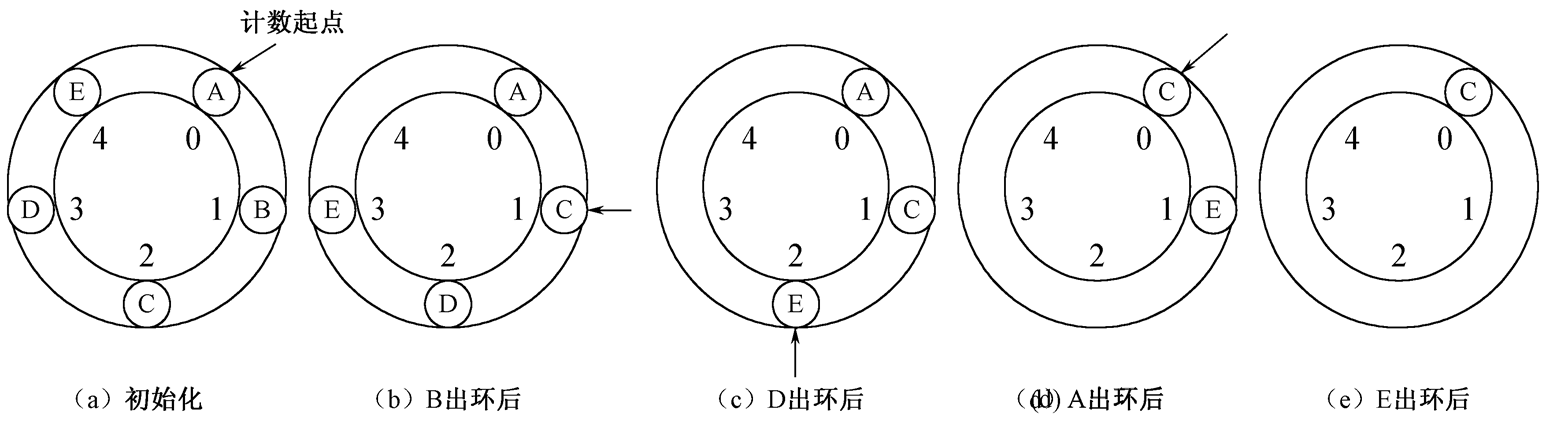
要求一:采用循环链表解决。
要求二:可以使用模拟法,模拟循环链表。
要求三:可以不使用循环链表类的定义使用方式。
输入描述
输入只有一行且为用空格隔开的三个正整数n,k,m,其含义如上所述。
输出描述
共 n 行,表示这 n 个人的出列顺序。
输入样例
3 5 8
输出样例
3
2
1
代码:
import java.util.*;
public class Main {
public static class Person {
int id;
Person next;
public Person() {}
public Person(int id) {
this.id = id;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
int m = sc.nextInt();
Person first = new Person();
Person curPerson = null;
for (int i = 1; i <= n; i++) {
Person person = new Person(i);
//第一个人
if (i == 1) {
first = person;
first.next = person;
curPerson = first;
}
//构成环链
else {
curPerson.next = person;
person.next = first;
curPerson = person;
}
}
//创建辅助指针,用来判断环是否只剩一个人
Person last = first;
while (true) {
//辅助指针指向最后一个人
if (last.next == first) {
break;
}
last = last.next;
}
//指向第一个开始报数的人
for (int i = 1; i < k; i++) {
first = first.next;
last = last.next;
}
//开始报数
while (true) {
//环中只有一个人
if (last == first) {
break;
}
for (int i = 1; i < m; i++) {
first = first.next;
last = last.next;
}
//出圈
System.out.println(first.id);
first = first.next;
last.next = first;
}
System.out.println(first.id);
}
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若内容造成侵权/违法违规/事实不符,请联系邮箱:jacktools123@163.com进行投诉反馈,一经查实,立即删除!
标签:

