首页 > 基础资料博客日记

2023第十四届蓝桥杯Java B组个人题解

2023-07-24 10:43:32基础资料围观413次

这篇文章介绍了2023第十四届蓝桥杯Java B组个人题解，分享给大家做个参考，收藏Java资料网收获更多编程知识

💎蓝桥杯系列文章

欢迎大家阅读蓝桥杯文章专栏🍄🍄

🔥2023第十四届蓝桥杯模拟赛第二期个人题解（Java实现）
🔥2023第十四届蓝桥杯模拟赛第三期个人题解（Java实现）
🔥蓝桥杯备赛之动态规划篇——背包问题
🔥蓝桥杯备赛之动态规划篇——涂色问题（区间DP）
🔥蓝桥杯真题——单词分析（Java实现）

💎第十四届蓝桥杯Java B组真题

💎蓝桥杯系列文章
💎前言
💎Part I 填空题
💎Part II 编程题
💎总结

💎前言

😘😘哈喽，大家好！今年的蓝桥杯终于落下帷幕啦！今天真的被整得怀疑人生了😭😭😭😭今年主打的就是陪伴😪赛后我重新做了这些题，写下这篇题解，跟大家交流交流！🍄

🙊🙊如果我写的内容有误，欢迎大家在评论区指正👏希望这篇文章对你有帮助❤❤同时欢迎关注我呦👇👇

雾霾愈让人窒息，我愈拼命争取一口清新；
黑暗愈遮盖大地，我们的心看得就愈清晰！

💎Part I 填空题

🎯试题 A: 阶乘求和

问题描述
　　令 S = 1! + 2! + 3! + … + 202320232023!，求 S 的末尾 9 位数字。
　　提示：答案首位不为 0。
答案提交
　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🌞问题分析

🍒🍒这道题肯定不能按题目的要求算到 202320232023!，肯定有规律可循，所以不妨先算前50项，取最后9位看看结果。阶乘算出来的结果很大，用Long也会爆，可以用BigIneger，需要注意的是BigInteger的加减乘除需要调API实现。

💡Java代码

import java.math.BigInteger;

public class 试题A_阶乘求和 {

	public static void main(String[] args) {
		BigInteger n=new BigInteger("1");
		BigInteger sum=new BigInteger("0");
		for(int i=1;i<50;i++) {
			n=n.multiply(new BigInteger(""+i));
			sum=sum.add(n);
			System.out.println("i="+i+"时，sum后九位是："+sum.mod(new BigInteger(""+1000000000)));
		}
	}
}

💯结果

i=1时，sum后九位是：1
i=2时，sum后九位是：3
i=3时，sum后九位是：9
i=4时，sum后九位是：33
i=5时，sum后九位是：153
i=6时，sum后九位是：873
i=7时，sum后九位是：5913
i=8时，sum后九位是：46233
i=9时，sum后九位是：409113
i=10时，sum后九位是：4037913
i=11时，sum后九位是：43954713
i=12时，sum后九位是：522956313
i=13时，sum后九位是：749977113
i=14时，sum后九位是：928268313
i=15时，sum后九位是：602636313
i=16时，sum后九位是：392524313
i=17时，sum后九位是：820620313
i=18时，sum后九位是：526348313
i=19时，sum后九位是：935180313
i=20时，sum后九位是：111820313
i=21时，sum后九位是：821260313
i=22时，sum后九位是：428940313
i=23时，sum后九位是：405580313
i=24时，sum后九位是：844940313
i=25时，sum后九位是：828940313
i=26时，sum后九位是：412940313
i=27时，sum后九位是：180940313
i=28时，sum后九位是：684940313
i=29时，sum后九位是：300940313
i=30时，sum后九位是：780940313
i=31时，sum后九位是：660940313
i=32时，sum后九位是：820940313
i=33时，sum后九位是：100940313
i=34时，sum后九位是：620940313
i=35时，sum后九位是：820940313
i=36时，sum后九位是：20940313
i=37时，sum后九位是：420940313
i=38时，sum后九位是：620940313
i=39时，sum后九位是：420940313
i=40时，sum后九位是：420940313
i=41时，sum后九位是：420940313
i=42时，sum后九位是：420940313
i=43时，sum后九位是：420940313
i=44时，sum后九位是：420940313
i=45时，sum后九位是：420940313
i=46时，sum后九位是：420940313
i=47时，sum后九位是：420940313
i=48时，sum后九位是：420940313
i=49时，sum后九位是：420940313
i=50时，sum后九位是：420940313

💯💯结果可以发现，从第39项开始，最后9位数字就没有变化了，所以答案就是420940313

🎯试题 B: 幸运数字

问题描述
　　哈沙德数是指在某个固定的进位制当中，可以被各位数字之和整除的正整数。例如 126 是十进制下的一个哈沙德数，因为 (126)10 mod (1+2+6) = 0；126也是八进制下的哈沙德数，因为 (126)10 = (176)8，(126)10 mod (1 + 7 + 6) = 0；同时 126 也是 16 进制下的哈沙德数，因为 (126)10 = (7e)16，(126)10 mod (7 + e) = 0。小蓝认为，如果一个整数在二进制、八进制、十进制、十六进制下均为哈沙德数，那么这个数字就是幸运数字，第 1 至第 10 个幸运数字的十进制表示为：1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数字是多少？你只需要告诉小蓝这个整数的十进制表示即可。
答案提交
　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🌞 问题分析

🍒🍒 这道题目单纯考察进制转换，调用Java现成的API即可：
十进制转二进制：Integer.toBinaryString(i)
十进制转八进制：Integer.toOctalString(i)
十进制转十六进制：Integer.toHexString(i)
💥💥求数位之和要注意：十六进制字符串可能包含a-f,所以需要特殊处理。

💡Java代码

public class 试题B_幸运数字 {
	//求一个数字字符串的数位之和
	public static int getSum(String s) {
		int sum=0;
		for(int i=0;i<s.length();i++) {
			if(s.charAt(i)>='a'&&s.charAt(i)<='f') //如果是a-f
				sum+=s.charAt(i)-'a'+10;
			else //如果是数字
				sum+=s.charAt(i)-'0';
		}
		return sum;
	}
	public static void main(String[] args) {
		int count=0;
		for(int i=1;i<1000000;i++) {
			String a2=Integer.toBinaryString(i);	//转为二进制
			String a8=Integer.toOctalString(i);		//转为八进制
			String a16=Integer.toHexString(i);		//转为十六进制
			if(i%getSum(a2)==0&&i%getSum(a8)==0&&i%getSum(a16)==0&&i%getSum(""+i)==0) {
				count++;
				if(count==2023) {
					System.out.println("第 2023 个幸运数字是:"+i);
					break;
				}
			}	
		}
	}
}

💯 结果

第 2023 个幸运数字是:215040

💎Part II 编程题

🎯试题 C: 数组分割

问题描述
　　小蓝有一个长度为 N 的数组 A = [A0, A1, . . .，AN−1]。现在小蓝想要从 A 对应的数组下标所构成的集合 I = {0, 1, 2, . . . , N − 1} 中找出一个子集 R1，那么 R1在 I 中的补集为 R2。记 S1 = ∑ r ∈ R1 Ar，S2 = ∑ r ∈ R2 Ar，我们要求 S1 和 S2 均为偶数，请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将S 1 或 S 2 视为 0。
输入格式
　　第一行一个整数 T，表示有 T 组数据。
　　接下来输入 T 组数据，每组数据包含两行：第一行一个整数 N，表示数组A 的长度；第二行输入 N 个整数从左至右依次为 A0, A1, . . . , AN−1，相邻元素之间用空格分隔。
输出格式
　　对于每组数据，输出一行，包含一个整数表示答案，答案可能会很大，你需要将答案对 1000000007 进行取模后输出。
样例输入
　　2
　　2
　　6 6
　　2
　　1 6
样例输出
　　4
　　0
样例说明
　　对于第一组数据，答案为 4。（注意：大括号内的数字表示元素在数组中的下标。）
R1 = {0}, R2 = {1}；此时 S 1 = A0 = 6 为偶数, S 2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0}；此时 S 1 = A1 = 6 为偶数, S 2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {}；此时 S 1 = A0 + A1 = 12 为偶数, S 2 = 0 为偶数。
R1 = {}, R2 = {0, 1}；此时 S 1 = 0 为偶数, S 2 = A0 + A1 = 12 为偶数。
　　对于第二组数据，无论怎么选择，都不满足条件，所以答案为 0。
评测用例规模与约定
对于 20% 的评测用例，1 ≤ N ≤ 10。
对于 40% 的评测用例，1 ≤ N ≤ 102。
对于 100% 的评测用例，1 ≤ T ≤ 10, 1 ≤ N ≤ 103, 0 ≤ Ai ≤ 109。

🌞问题分析

🍓🍓 这道题我想到的是暴力解法。对于所给数组A（元素可重复），用回溯法求解出其所有的子集R1，将数组A的元素和 - 子集R1的元素和，即得到补集R2的元素和，然后判断是否满足条件。
💥💥 注意：将答案对 1000000007 进行取模后输出

💡 Java代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;
import java.util.stream.Collectors;

// 子集类
class SubSet{
	List<List<Integer>> res=new LinkedList<List<Integer>>();//存储所有子集
	LinkedList<Integer> track=new LinkedList<Integer>();	//存储一个子集
	boolean[] used;			//记录是否访问过
	// 求出所有子集
	List<List<Integer>> subset(int[] nums){
		used=new boolean[nums.length];
		backtrack(nums, 0);
		return res;
	}
	// 回溯法求子集
	void backtrack(int[] nums,int start) {
		res.add(new LinkedList<Integer>(track));
		//回溯框架
		for(int i=start;i<nums.length;i++) {
			//不用剪枝，可以重复
//			if(i>start&&nums[i]==nums[i-1]&&!used[i-1]))
//				continue;
			//选择
			used[i]=true;
			track.add(nums[i]);
			//进入下一层回溯
			backtrack(nums, i+1);
			//撤销选择
			track.removeLast();
			used[i]=false;
		}
		
	}
}
public class 试题C_数组分割 {
	//返回一个列表的所有数字的和
	public static int getSum(List<Integer> nums) {
		int sum=0;
		for(int e:nums)
			sum+=e;
		return sum;
	}
	//统计满足条件的R1个数
	public static int count(int[] A) {
		SubSet subSet=new SubSet();
		List<List<Integer>> resList=subSet.subset(A);
		int count=0;	//统计满足情况的R1个数
		for(List<Integer> R1:resList) {
			//将数组A转为List
			List<Integer> listA=Arrays.stream(A).boxed().collect(Collectors.toList());
			//R1的补集R2的元素和S2
			int S2=(getSum(listA)-getSum(R1))%2;
			if(getSum(R1)%2==0&&S2==0)
				count++;
		}
		return count%1000000007;
	}
	public static void main(String[] args) {
		//输入
		Scanner sc=new Scanner(System.in);
		int T=sc.nextInt();		//有T组数据
		int[] res=new int[T];	//记录每组数据的结果
		for(int i=0;i<T;i++) {
			int N=sc.nextInt();
			int[] A=new int[N];	//存放每组数据
			for(int j=0;j<N;j++) {
				A[j]=sc.nextInt();
			}
			res[i]=count(A);
		}
		for(int i=0;i<T;i++) {
			System.out.println(res[i]);
		}
	}
}

🎯试题 D: 矩形总面积

问题描述
　　平面上有个两个矩形 R1 和 R2，它们各边都与坐标轴平行。设 (x1, y1) 和(x2, y2) 依次是 R1 的左下角和右上角坐标，(x3, y3) 和 (x4, y4) 依次是 R2 的左下角和右上角坐标，请你计算 R1 和 R2 的总面积是多少？
　　注意：如果 R1 和 R2 有重叠区域，重叠区域的面积只计算一次。
输入格式
　　输入只有一行，包含 8 个整数，依次是：x1，y1，x2，y2，x3，y3，x4 和 y4。
输出格式
　　一个整数，代表答案。
样例输入
　　2 1 7 4 5 3 8 6
样例输出
　　22
评测用例规模与约定
对于 20% 的数据，R1 和 R2 没有重叠区域。
对于 20% 的数据，其中一个矩形完全在另一个矩形内部。
对于 50% 的数据，所有坐标的取值范围是 [0, 10^3]。
对于 100% 的数据，所有坐标的取值范围是 [0, 10^5]。

🌞问题分析

🍉🍉这道题是纯数学模拟题。总共分三种情况：

R1和R2完全不重合
矩形总面积=R1的面积+R2的面积
R1完全在R2内部或R2完全在R1内部
矩形总面积=R1的面积或R2的面积
R1和R2有部分重叠
矩形总面积=R1的面积+R2的面积-重叠部分的面积
这种情况单纯列举的话，要判断8种情况（如下图），很麻烦。。。

然后我列举其中几种情况，写出表达式以后，发现了一个规律：
将x={x1,x2,x3,x4}和y={y1,y2,y3,y4}分别从小到大排序，重叠部分面积=(x[2]-x[1])*(y[2]-y[1]),这样就不用列举8种情况啦！感兴趣的同学可以试试验证一下！
注意：对于 100% 的数据，所有坐标的取值范围是 [0, 10^5]，所以记得开long,不然就爆啦！

💡 Java代码

import java.util.Arrays;
import java.util.Scanner;

public class 试题D_矩形总面积 {

	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		long x1=sc.nextLong();
		long y1=sc.nextLong();
		long x2=sc.nextLong();
		long y2=sc.nextLong();
		long x3=sc.nextLong();
		long y3=sc.nextLong();
		long x4=sc.nextLong();
		long y4=sc.nextLong();
		long res=0L;
		//R1 和 R2 没有重叠区域
		if(x2<=x3||x1>=x4||y2<=y3||y1>=y4) {
			res=(x2-x1)*(y2-y1)+(x4-x3)*(y4-y3);
			System.out.println(res);
		}
		//R2完全在R1内部
		else if(x1<=x3&&x4<=x2&&y1<=y3&&y4<=y2) {
			res=(x2-x1)*(y2-y1);
			System.out.println(res);
		}
		//R1完全在R2内部
		else if(x3<=x1&&x2<=x4&&y3<=y1&&y2<=y4) {
			res=(x4-x3)*(y4-y3);
			System.out.println(res);
		}
		//R1和R2有部分重叠
		else {
			long[] x= {x1,x2,x3,x4};
			long[] y= {y1,y2,y3,y4};
			Arrays.sort(x);
			Arrays.sort(y);
			//减去重复部分的面积
			res=(x2-x1)*(y2-y1)+(x4-x3)*(y4-y3)-(x[2]-x[1])*(y[2]-y[1]);
			System.out.println(res);
		}
	}

}

🎯试题 F: 合并区域

问题描述
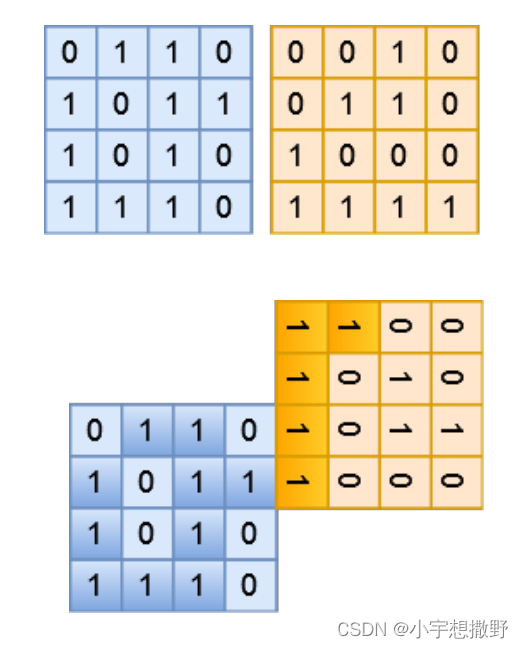
　　小蓝在玩一款种地游戏。现在他被分配给了两块大小均为 N × N 的正方形区域。这两块区域都按照 N × N 的规格进行了均等划分，划分成了若干块面积相同的小区域，其中每块小区域要么是岩石，要么就是土壤，在垂直或者水平方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进行合并，他想知道合并以后可以得到的最大的一块土地的面积是多少（土地的面积就是土地中土壤小区域的块数）？
　　在进行合并时，小区域之间必须对齐。可以在两块方形区域的任何一条边上进行合并，可以对两块方形区域进行 90 度、180 度、270 度、360 度的旋转，但不可以进行上下或左右翻转，并且两块方形区域不可以发生重叠。
输入格式
　　第一行一个整数 N 表示区域大小。
　　接下来 N 行表示第一块区域，每行 N 个值为 0 或 1 的整数，相邻的整数之间用空格进行分隔。值为 0 表示这块小区域是岩石，值为 1 表示这块小区域是土壤。
　　再接下来 N 行表示第二块区域，每行 N 个值为 0 或 1 的整数，相邻的整数之间用空格进行分隔。值为 0 表示这块小区域是岩石，值为 1 表示这块小区域是土壤。
输出格式
　　一个整数表示将两块区域合并之后可以产生的最大的土地面积。
样例输入
　　4
　　0 1 1 0
　　1 0 1 1
　　1 0 1 0
　　1 1 1 0
　　0 0 1 0
　　0 1 1 0
　　1 0 0 0
　　1 1 1 1
样例输出
　　15
样例说明

第一张图展示了样例中的两块区域的布局。第二张图展示了其中一种最佳的合并方式，此时最大的土地面积为 15。
评测用例规模与约定
对于 30% 的数据，1 ≤ N ≤ 5。
对于 60% 的数据，1 ≤ N ≤ 15。
对于 100% 的数据，1 ≤ N ≤ 50。

🌞问题分析

🍉🍉这道题可以用深度优先搜索。（比赛时默写了深搜模板不会用💦💦）一开始看到题目说区域可以进行90 度、180 度、270 度、360 度的旋转，被这个干懵圈了😭😭现在想想其实不用管这个，合并区域的最大面积就是找两个区域四周边缘土地的最大面积之和，所以在每个区域中，利用深度优先搜索，从上下左右四个边缘寻找最大面积的土地（在区域中央的封闭土地就不用理了）。
📢📢这道题和岛屿问题差不多，感兴趣的小伙伴可以看看力扣的这几道题。
👉力扣 695. 岛屿的最大面积
👉力扣 1254. 统计封闭岛屿的数目
👉力扣 200. 岛屿数量

💡 Java代码

import java.util.Scanner;

public class 试题F_合并区域 {
	// 将(x,y)所在的土地变成岩石，并返回该土地面积
	public static int dfs(int[][] grid,int x,int y) {
		int m=grid.length,n=grid[0].length;
		// 超出区域边界
		if(x<0||x>=m||y<0||y>=n) 
			return 0;
		// 如果已经是岩石了
		if(grid[x][y]==0)
			return 0;
		// 将土壤变成岩石
		grid[x][y]=0;
		return dfs(grid, x, y+1)+dfs(grid, x+1, y)+dfs(grid, x, y-1)+dfs(grid, x-1, y)+1;
		
	}
	// 记录合并区域的最大面积
	public static int maxArea(int[][] grid) {
		int m=grid.length,n=grid[0].length;
		int res=0;
		for(int i=0;i<m;i++) {
			// 将区域上边缘的土壤变成岩石，并记录土地的最大面积
			res=Math.max(res, dfs(grid, 0, i));
			// 将区域下边缘的土壤变成岩石，并记录土地的最大面积
			res=Math.max(res,dfs(grid, m-1, i));
		}
		for(int j=0;j<n;j++) {
			// 将区域左边缘的土壤变成岩石，并记录土地的最大面积
			res=Math.max(res, dfs(grid, j, 0));
			// 将区域右边缘的土壤变成岩石，并记录土地的最大面积
			res=Math.max(res, dfs(grid, j, n-1));
		}
		return res;
	}
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int N=sc.nextInt();	//区域大小
		int[][] grid1=new int[N][N];
		int[][] grid2=new int[N][N];
		// 输入区域1
		for(int i=0;i<N;i++) 
			for(int j=0;j<N;j++) 
				grid1[i][j]=sc.nextInt();
		// 输入区域1
		for(int i=0;i<N;i++) 
			for(int j=0;j<N;j++) 
				grid2[i][j]=sc.nextInt();
		System.out.println(maxArea(grid1)+maxArea(grid2));
	}

}

💎总结

💖💖目前先写这几道题的题解，后续有时间的话再写剩余的题解！
🌈🌈有问题的地方希望大家指正呀💗如果你觉得这篇文章对你有帮助，欢迎点赞评论收藏，或者关注我呦！！！爱你们😘

文章来源:https://blog.csdn.net/weixin_51627036/article/details/130034406
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！

标签：

上一篇：谷歌浏览器F12开发者工具NETWORK的用法详解
下一篇：WebSecurityConfigurerAdapter已弃用

首页 > 基础资料博客日记

2023第十四届蓝桥杯Java B组个人题解

💎蓝桥杯系列文章

💎第十四届蓝桥杯Java B组真题

💎前言

💎Part I 填空题

🎯试题 A: 阶乘求和

🌞问题分析

💡Java代码

💯结果

🎯试题 B: 幸运数字

🌞 问题分析

💡Java代码

💯 结果

💎Part II 编程题

🎯试题 C: 数组分割

🌞问题分析

💡 Java代码

🎯试题 D: 矩形总面积

🌞问题分析

💡 Java代码

🎯试题 F: 合并区域

🌞问题分析

💡 Java代码

💎总结

相关文章

最新发布

点击排行

本站推荐

标签云

首页 > 基础资料 博客日记

2023第十四届蓝桥杯Java B组个人题解

💎蓝桥杯系列文章

💎第十四届蓝桥杯Java B组真题

💎前言

💎Part I 填空题

🎯试题 A: 阶乘求和

🌞问题分析

💡Java代码

💯结果

🎯试题 B: 幸运数字

🌞 问题分析

💡Java代码

💯 结果

💎Part II 编程题

🎯试题 C: 数组分割

🌞问题分析

💡 Java代码

🎯试题 D: 矩形总面积

🌞问题分析

💡 Java代码

🎯试题 F: 合并区域

🌞问题分析

💡 Java代码

💎总结

相关文章

最新发布

点击排行

本站推荐

标签云

首页 > 基础资料博客日记