首页 > 基础资料 博客日记
树(Tree)和二叉树
2023-11-21 18:01:06基础资料围观648次
目录
1.树的定义
树是一种非线性的数据结构,它表现的关系是一对多
它是由n(n>=0)个结点组成的有限集,当n = 0时,称为空树。
在任意一棵非空树中应满足:
1.有且仅有一个特殊的根节点,根节点没有前驱结点
2.每一个非根结点有且只有一个父结点;
除了根结点外,每个子结点可以分为多个不相交的子树,并且子树是不相交的
3.树是递归定义的
4.一颗N个结点的树有N-1条边
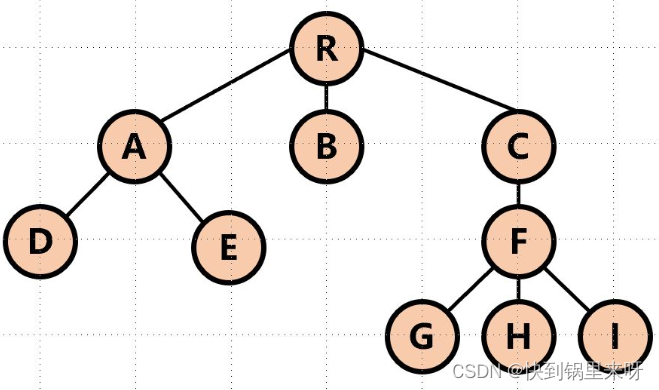
2.一些树的关键词定义
结点的度:一个结点含有子树的个数称为该结点的度树的度:一棵树中,所有结点度的最大值称为树的度树的深度:一棵树中节点的最大深度就是树的深度,也称为高度父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点
子节点:一个节点含有的子树的根节点称为该节点的子节点
节点的层次:从根节点开始,根节点为第一层,根的子节点为第二层,以此类推
兄弟节点:拥有共同父节点的节点互称为兄弟节点
叶子节点:度为零的节点就是叶子节点
祖先:从根到该结点所经分支上的所有结点;
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
森林:m颗互不相交的树构成的集合就是森林
3.树的存储结构
(1)双亲表示法(2)孩子表示法(3)孩子兄弟表示法
(1)双亲表示法
在每个节点中,有一个指示器指示其双亲结点到链表中的位置,
使其每个结点,不但知道自己是谁,而且知道双亲位置

(2)孩子表示法
将每个结点的孩子结点排序,以单链表存储,则n个结点有n个孩子链表
并且如果是叶子结点,这个单链表为空
然后将每个单链表的头指针组成一个线性表,顺序存储放入数组中
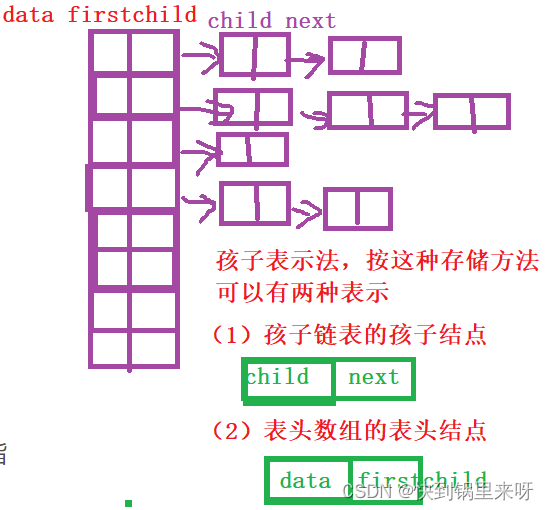
(3)孩子兄弟表示法
任意一棵树, 它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。 因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
这样也就把这个树变成了二叉树

4.二叉树的定义
二叉树是结点的一个有限集合,该集合为空,或者是由一个根节点加上两棵称为左子树和右子树的二叉树组成。
需要注意的是
(1)每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
(2)二叉树是有序树有左右之分,其子树的次序不能颠倒。
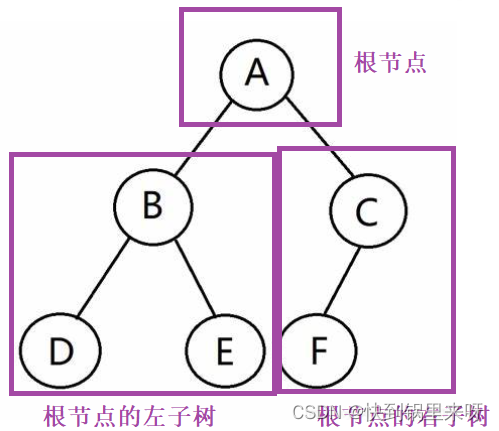
5.满二叉树和完全二叉树
(1)满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
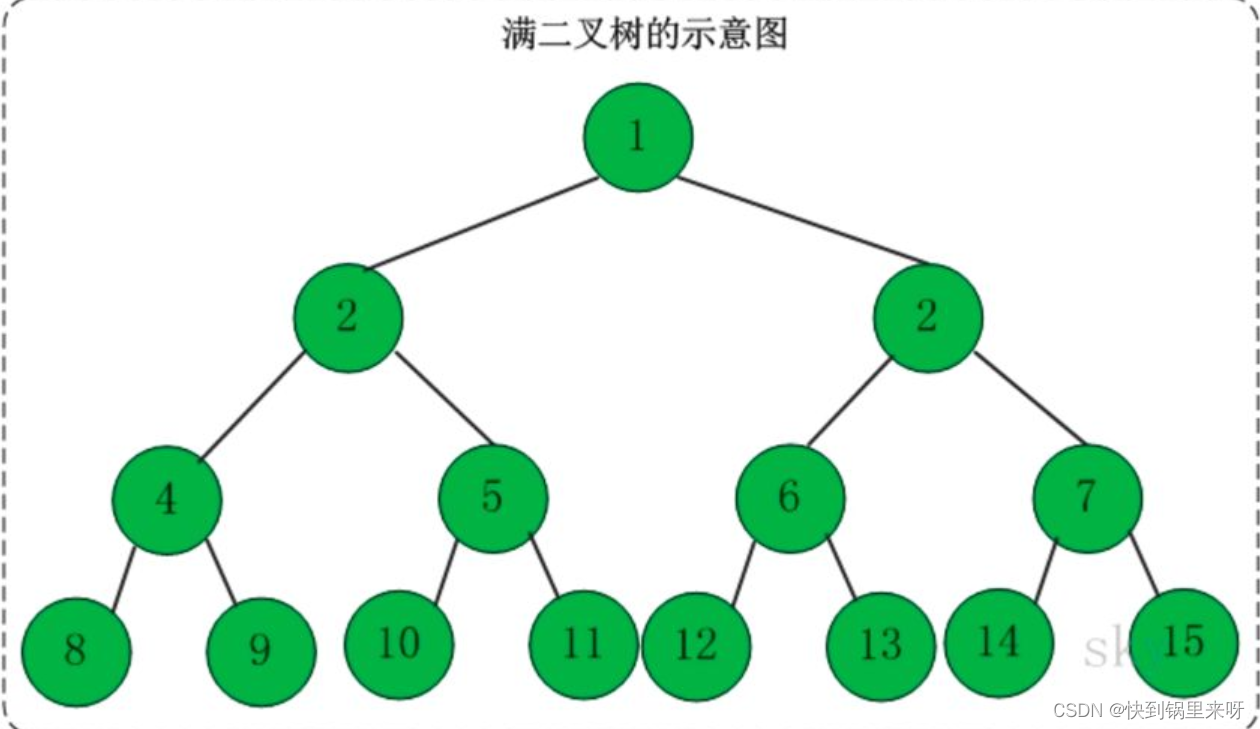
特点
- 满二叉树中第 i 层的节点数为 2n-1 个。
- 深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
(2)完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
满二叉树是一种特殊的完全二叉树
n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
6.二叉树的性质
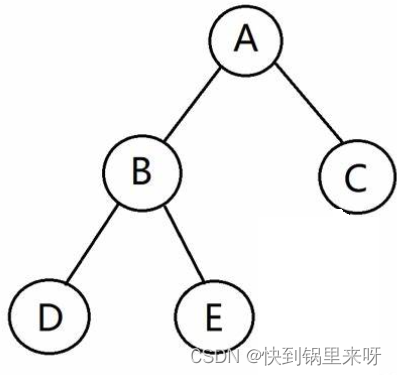
(1)在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
(2)深度为k的二叉树至多有2^k-1个结点(k>=1)
可以看上面的图,深度为4,一共有2^4 -1= 15个结点
(3)对于任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1
(4)具有n个节点的完全二叉树深为log2x+1(其中x表示不大于n的最大整数)
(5)如果对一颗有n个结点的完全二叉树(其深度为[log2n]+1)的结点按层序编号(从 层到[log2n]+1层,每层从左到右),对任一结点i(1<=i<=n):
如果i=1,则结点i是二叉树的根,无双亲,如果i>1,则其双亲结点是结点[i/2]
如果2i>n,则结点i无左孩子(结点i为叶子结点)否则左孩子是结点2i。
如果2i+1>n,则结点i无右孩子,否则其右孩子是结点2i+1.
下面看几个练习题
1.在具有 2n 个结点的完全二叉树中,叶子结点个数为( A )
A nB n+1C n-1D n/2一共有2n个结点 也就是偶数个结点,那么一定存在一个度为1的结点所以就有 2n = n0+n2+1 n0 = n2+1所以就有 2n = n0+n0-1+1 --->n = n02. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B )A 不存在这样的二叉树B 200C 198D 199n2 = 199 n0=n2+1=2003.一棵完全二叉树的节点数为531个,那么这棵树的高度为( B )A 11B 10C 8D 12k=log2 531 +1 取104.一个具有767个节点的完全二叉树,其叶子节点个数为( B )A 383B 384C 385D 386767个结点 是奇数,那么度为1的结点没有所以就是 767 = n0+n2 n0 = n2+1所以就有767 = n0+n0-1 n0 = 384
7.二叉树的存储方式
二叉树的存储方式有 顺序存储和类似于链表的链式存储
二叉树的类似于链式存储是,一个一个节点引用起来的,这两种具体结构前面树已经提过了
(1)孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}(2)孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}8.二叉树的基本操作
8.1 二叉树的4种遍历方式
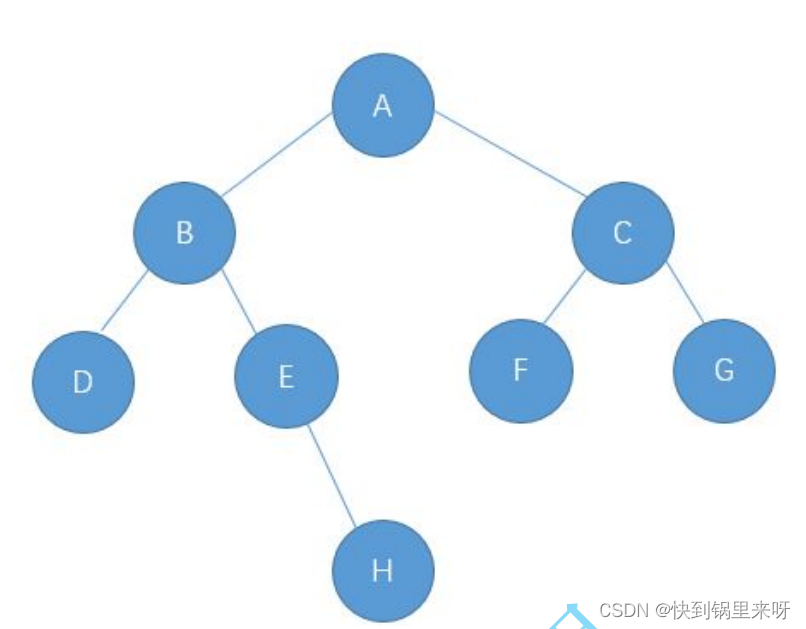
用代码将上面的这个二叉树结构穷举一遍
static class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
//二叉数的根节点
public TreeNode root;
public void createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
this.root = A;
}(1)前序遍历(根-->左-->右)
先访问一棵树的根节点,再访问左子树,最后访问右子树。
上面的遍历次序就是 A -> B -> D -> E -> H -> C -> F -> G
void preOrder(TreeNode root) {
if (root == null) return;
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}(2)中序遍历(左-->根-->右)
先访问一棵树的左子树,再访问根节点,最后访问右子树。
上面的遍历次序就是 D -> B -> E -> H -> A -> F -> C -> G
void inOrder(TreeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}(3)后序遍历(左-->右-->根)
先访问一棵树的左子树,再访问右子树,最后访问根节点。
上面的遍历次序就是 D -> H -> E -> B -> F -> G -> C -> A
void postOrde(TreeNode root) {
if (root == null) return;
postOrde(root.left);
postOrde(root.right);
System.out.print(root.val + " ");
}(4)层序遍历
先访问第一层的根结点,然后从左到右访问第2层上的节点,接着访问第三层的结点。
8.2 二叉树的基本操作
(1)获取树中结点的个数size()
两种思路
子问题:先遍历左边的树,再遍历右边的树,不为null就++
遍历递归思路:只要不为null就给sizeNode++
//1.子问题思路
int size(TreeNode root) {
if(root == null) return 0;
return size(root.left) + size(root.right) + 1;
}
//2.遍历递归思路
public static int sizeNode;
void size2(TreeNode root){
if(root == null) return;
sizeNode++;
size2(root.left);
size2(root.right);
}(2)获取叶子结点的个数getLeafNodeCount()
还是两种思路
子问题:左树的叶子+右树的叶子 = 整棵树的叶子
遍历递归思路:遍历到叶子就++
判断是不是叶子的条件是root.left == null && root.right == nul
//1.子问题
int getLeafNodeCount(TreeNode root){
if(root == null) return 0;
if (root.left == null && root.right == null) {
return 1;
}
return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}
//2.遍历递归
public static int leafSize;
void getLeafNodeCount2(TreeNode root){
if(root == null) return ;
if (root.left == null && root.right == null) {
leafSize++;
}
getLeafNodeCount2(root.left);
getLeafNodeCount2(root.right);
}(3)获取第K层结点的个数getKLevelNodeCount()
int getKLevelNodeCount(TreeNode root, int k) {
if(root == null) return 0;
if (k == 1) {
return 1;
}
return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);
}
(4)获取二叉树的高度getHeight()\
二叉树的高度--》左树高度和右树高度最大值+1
int getHeight(TreeNode root) {
if(root == null) return 0;
int leftHight = getHeight(root.left);
int rightHight = getHeight(root.right);
return (leftHight > rightHight ?
leftHight + 1 :
rightHight + 1);
}时间复杂度O(N)
(5)检测值为value的元素是否存在fifind()
先看根是不是要找到元素,如果不是在左子树找,还不是就右子树找
TreeNode find(TreeNode root, int val) {
if(root == null) return null;
if(root.val == val) {
return root;
}
TreeNode ret1 = find(root.left,val);
if (ret1 != null) {
return ret1;
}
TreeNode ret2 = find(root.right,val);
if (ret2 != null) {
return ret2;
}
return null;
}(6)层序遍历levelOrder()

void levelOrder(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
//现将根节点放进队列中
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
//只要子树的左右节点不为null就给队列里面放
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
System.out.println();
}(7)判断一颗树是不是完全二叉树isCompleteTree()
在判断一颗树是不是完全二叉树前,先要明白,给队列中放元素放null
此时这个队列不为null

boolean isCompleteTree(TreeNode root) {
if (root == null) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
queue.offer(cur.left);
queue.offer(cur.right);
}else {
break;
}
}
while(!queue.isEmpty()) {
TreeNode cur = queue.peek();
if (cur != null) {
return false;
}else {
queue.poll();
}
}
return true;
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若内容造成侵权/违法违规/事实不符,请联系邮箱:jacktools123@163.com进行投诉反馈,一经查实,立即删除!
标签:




