首页 > 面试资料博客日记

PriorityQueue 数据结构底层原理、源码实现可视化分析及应用实战

2025-09-01 02:30:02面试资料围观174次

文章PriorityQueue 数据结构底层原理、源码实现可视化分析及应用实战分享给大家，欢迎收藏Java资料网，专注分享技术知识

本文将从数据结构底层原理 + 源码实现 + 应用实战三方面深入剖析 PriorityQueue，让你真正掌握优先队列的底层逻辑及其应用。

源码可视化视频：https://www.bilibili.com/video/BV12Ha5zjEcS/

在玩游戏的时候，发现需要购买的装备很多，而且不同的英雄需要购买的装备还不一样，打游戏的时候需要更多精力去关注买什么装备才行。这多少影响游戏体验，特别是我这种小白，打开装备栏挑了半天没找到自己要买的，然后就嘎了_^。游戏难度太大（体验太差）玩不来，卸载了吧。

如果开始游戏前就先配置好我要玩的英雄的装备购买顺序，那岂不美哉。打游戏的时候，游戏自动提示你要购买的装备，直到你全部装备都买好了。

通过PriorityQueue便可轻松实现上面想要的功能。

开始游戏前配置装备优先级的过程为：入队操作过程；

打游戏提示购买装备顺序的过程为：出队操作过程。

文中实战部分会讲到这个案例如何实现，我们先从最简单的是什么开始。

🚀 1. 概述

1.1. PriorityQueue 是什么？

PriorityQueue 是一个 优先级的队列，元素按优先级从小到大排列（默认使用自然顺序，也可以传入比较器 Comparator）。

它并不保证 FIFO 顺序，也不保证整个队列有序，而是每次出队时返回当前优先级最高的元素。说白了，仅保证每次出队的元素是最大值或最小值，默认是最小值。

1.2. 底层数据结构

PriorityQueue 使用一个动态数组来维护数据，底层处理逻辑为二叉堆，默认为小顶堆。

学习PriorityQueue底层原理，就是学习怎么应用二叉堆实现优先队列。

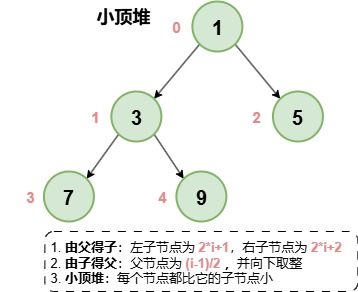
二叉堆为完全二叉树，按照从上到下、从左到右的顺序进行入堆，并且仅有最底层可能没有填满。

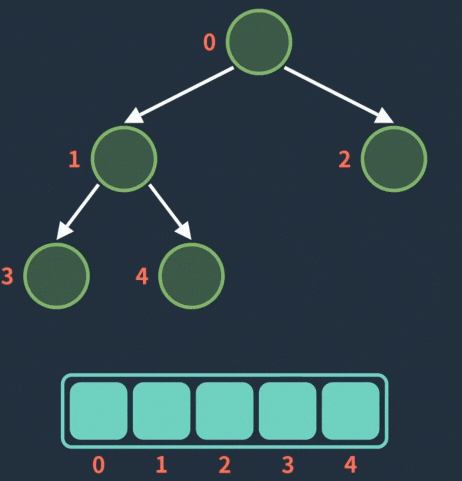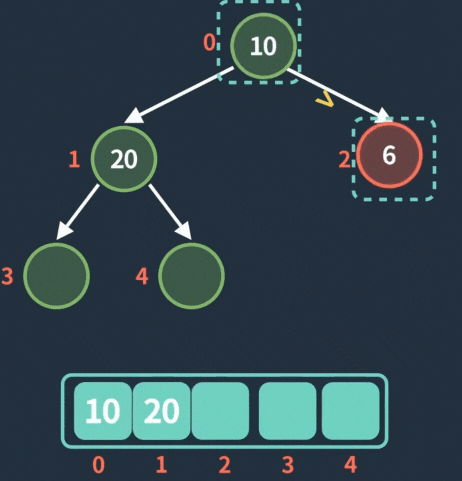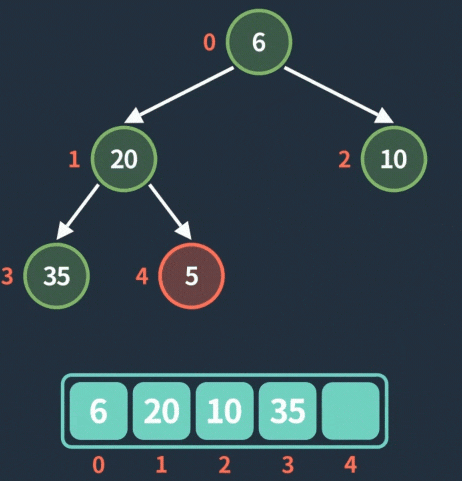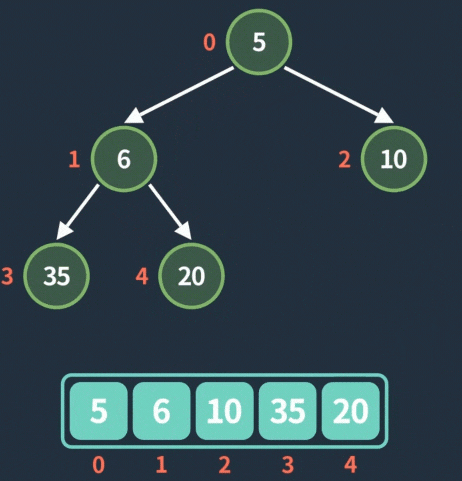
假设当前堆如下（PriorityQueue 数组下标从 0 开始）：

PriorityQueue层次遍历

在数组中的保存顺序为二叉树的层序遍历顺序：从根节点开始，从上到下、从左到右一个个遍历。

所以在数组表示为：[1, 3, 5, 7, 9]

1.3. 二叉堆的规律

这些规律将决定你的代码怎么去实现。

PriorityQueue的下标i是从0 开始计算的，以下公式也是基于i=0才成立的。

规律1，根据父节点计算子节点：父节点下标 i，那么左子节点就为 2*i+1，右子节点为 2*i+2。

反过来，如果左子节点为i，那么父节点为(i-1)/2；如果右子节点为i，那么父节点为(i-2)/2;

计算父结点一定要两个公式？？

左右节点相差1，必然会有一个是不能整除。

比如：左节点i=1,那么右节点必为i=2，父节点为0。

如果使用公式(i-1)/2，那么左节点计算结果为0，右节点计算为0.5，只需要向下取整即可。

如果使用公式(i-2)/2，那么左节点计算结果为-0.5，右节点计算为0，发现怎么取整都不可以。

规律2，根据子节点计算父节点：使用公式(i-1)/2计算并向下取整即可。

规律3，小顶堆/最小堆的每个节点都比它的子节点小；大顶堆/最大堆的每个节点都比它的子节点大。

PriorityQueue规律

⚙️ 2. 入队相关操作

上面的规律如果明白了，那下面的源码就很好明白了。

2.1. 入队操作

先明确知道，插入节点的入堆顺序是按照层序遍历从上到下、从左到右，就像你写作文一样从左到右➡，从上到下⬇地编写，也就是每次都放在数组元素的末端。

再结合小顶堆规律和二叉堆的计算公式：由子得父的简单计算公式。

涉及的关键源码：offer(e) 和 siftUp。

// 入队操作
public boolean offer(E e) {
	if (e == null)
		throw new NullPointerException();
	modCount++;
	int i = size;
    // 容量满后才扩容
	if (i >= queue.length)
		grow(i + 1);
	size = i + 1;
	if (i == 0)
		queue[0] = e;
	else
		siftUp(i, e);
	return true;
}
// siftUp 上浮
private void siftUp(int k, E x) {
	if (comparator != null)
		// 使用了自定义比较器
		siftUpUsingComparator(k, x);
	else
		// 使用类中的比较器
		siftUpComparable(k, x);
}
// siftUp 源码逻辑（有 Comparator 时）
private void siftUpUsingComparator(int k, E x) {
	while (k > 0) {
		// 由子节点 计算出 父节点数组索引
		int parent = (k - 1) >>> 1;
		// 获取父节点对象
		Object e = queue[parent];
		// 比较大小：儿子>=父亲 就没得玩了
		if (comparator.compare(x, (E) e) >= 0)
			break;
		// 儿子低位还小，继续上位，把老父亲换下去
		queue[k] = e;
		// 更新索引，继续比较
		k = parent;
	}
	// 最终看实力上位到 k 位置，坐好
	queue[k] = x;
}

使用了规律2（公式(i-1)/2计算，并向下取整），根据子节点计算父节点索引。

但源码的计算公式为：parent = (k - 1) >>> 1。

源码采用无符号右移一位，相当于除于2，但位移运算余数不会被保存，也就无需向下取整

比如：k=4，那么k-1=3，3 的二进制为11，右移一位变为1。

位移运算只会有整数部分参与运算，结果也只会有整数部分。

入队操作动图：

入队操作

2.2. 扩容操作

底层数据结构为数组，扩容操作跟ArrayList 基本一致。

扩容操作很简单，主要分为两步：计算新容量和元素拷贝。

Priority和ArrayList的扩容主要区别为：容量计算有一点点差异。

在容量小于64前，Priority 扩容的新容量为：翻倍+2；后面的扩容都一致为：增加 50%容量。增长量 = oldCapacity >> 1，即 oldCapacity/2（向下取整）。

具体源码如下：

// 扩容
private void grow(int minCapacity) {
	int oldCapacity = queue.length;
	// 计算新容量
	int newCapacity = oldCapacity + ((oldCapacity < 64) ?
									 (oldCapacity + 2) :
									 (oldCapacity >> 1));
	// 防止溢出
	if (newCapacity - MAX_ARRAY_SIZE > 0)
		newCapacity = hugeCapacity(minCapacity);
	// 拷贝元素到新数组
	queue = Arrays.copyOf(queue, newCapacity);
}
// 防止溢出
private static int hugeCapacity(int minCapacity) {
	if (minCapacity < 0) // overflow
		throw new OutOfMemoryError();
	return (minCapacity > MAX_ARRAY_SIZE) ?
		Integer.MAX_VALUE :
		MAX_ARRAY_SIZE;
}

🗑 3. 出队操作

出队操作分为三步：取堆顶，替堆顶，沉堆顶

取出堆的根节点--堆顶，即数组的第一个元素；

然后用最后一个节点替代堆顶；

堆顶下沉操作，最后取左右子节点最小的跟父节点比较，父大于子，则交换节点，完成堆顶下沉。

具体源码如下：

// 出队操作
public E poll() {
	if (size == 0)
		return null;
	int s = --size;
	modCount++;
	// 取出堆顶
	E result = (E) queue[0];
	// 用最后一个元素替代堆顶
	E x = (E) queue[s];
	// 移除最后一个节点
	queue[s] = null;
	if (s != 0)
		// 替代堆顶节点下沉
		siftDown(0, x);
	return result;
}
// 下沉恢复堆结构
private void siftDown(int k, E x) {
	if (comparator != null)
		siftDownUsingComparator(k, x);
	else
		siftDownComparable(k, x);
}
// 下沉调整恢复堆结构
private void siftDownUsingComparator(int k, E x) {
	// 大小除于2，half 为第一个 叶 子 节点
	int half = size >>> 1;
	// k 不是叶子节点，才需要上浮
	while (k < half) {
		// 由父得子：此为左节点公式
		int child = (k << 1) + 1;
		Object c = queue[child];
		// 左加一，得右节点索引
		int right = child + 1;
		// 左右节点比较，取小的节点
		if (right < size &&
			comparator.compare((E) c, (E) queue[right]) > 0)
			c = queue[child = right];
		// 小儿子和冒牌顶替的父亲比较
		if (comparator.compare(x, (E) c) <= 0)
			break;
		// 下沉交换
		queue[k] = c;
		k = child;
	}
	// 保存到合适的位置
	queue[k] = x;
}

PriorityQueue 就是通过出队的方式实现优先级的。它可以只出队一部分，完成部分优先级操作；也可以全部都出队，此时出队结果便是堆排序结果。

认真看下源码，有没有发现什么端倪？？

为什么循环条件是while (k < half) ？

因为所有叶子节点都没有孩子，也就没有可以在下沉可说了。

出队操作动图：

出队操作

🏗️ 4. 批量建堆（heapify）

现在有n个元素，通过入队操作，一个个放入数组中，单个元素操作的时间复杂度为O(logn)，n 个元素的时间复杂度就变为O(n*logn)。

现在有个更高效的方式：批量建堆。当已有一整个数组时，采用一次建堆，时间复杂度为O(n)

批量建堆就像盖房子一样，从地基开始，一层一层的搭建好。

批量建堆的整体过程：自底向上、逐层建堆

详细的处理过程为：

先将元素直接全部拷贝到数组
再从最后一个非叶子节点开始逆层序遍历建堆，
对每个子树的堆顶节点做下沉操作，保证其子树满足小顶堆特性

当通过带初始集合的构造器创建 PriorityQueue 时，会执行一次 批量建堆，其核心代码在构造器末尾调用：

public PriorityQueue(Collection<? extends E> c) {
    // … 将 c.toArray() 填充到 queue[]
    this.size = queue.length;
    heapify();
}

4.1. heapify 源码逻辑

private void heapify() {
    int n = size;
    // 从最后一个非叶子节点开始，依次向下调整
    for (int i = (n >>> 1) - 1; i >= 0; i--) {
        siftDown(i, (E) queue[i]);
    }
}

这源码可能看得有点费劲，这样可能清晰点

private void heapify() {
    // 找到最后一个非叶节点
    int lastParent = (size >>> 1) - 1;
    // 从这个节点开始，往前遍历到根节点
    for (int i = lastParent; i >= 0; i--) {
        // 把 queue[i] “下沉”到它在子树中正确的位置
        siftDown(i, (E) queue[i]);
    }
}

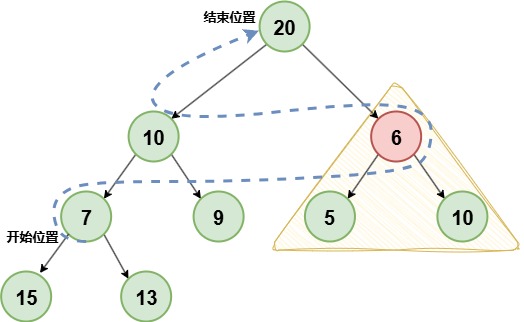
开始位置：由完全二叉树二叉堆的特性，可知最后一个非叶子节点下标为 (size >>> 1) - 1，这个索引往后的节点都是叶子节点，无需调整。

建堆过程：对每个节点调用 siftDown，保证其子树满足最小堆性质

建堆索引顺序图：

PriorityQueue建堆索引移动顺序

黄色三角形内只需要一次调平就可完成，然后继续往上逐层调整：

PriorityQueue建堆调平1

最后调整完成：

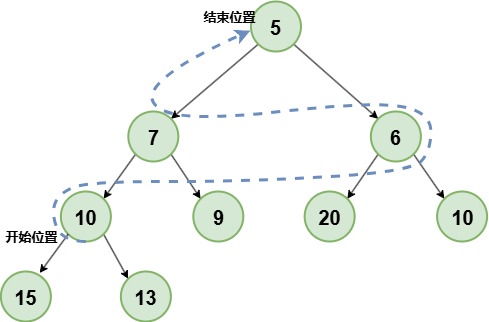
PriorityQueue建堆调平2

整个建堆过程为：从最后非叶子节点开始，自底向上，逐个下沉调整，直到堆顶。

批量建堆可视化：

批量建堆操作

哪可不可以从堆顶开始调整，自顶向下，逐层下沉调整？

4.2. 为什么自底向上更快？

如果采用从堆顶开始调整，自顶向下，逐层下沉调整会怎样？

4.2.1. 为什么选择自底向上、逐层下沉？

❌从堆顶开始调整，自顶向下，逐层下沉调整。当你在 i=0（根节点）做 siftDown 时，左右子树尚未调整，它们可能不是堆。尽管上层节点调整好了，之后再去调整下层节点时，又可能会破坏你先前在上层建立的堆序性，最终很可能得到一个不合法的堆。如果要确保每层都合法，那就得重复计算上层已经调整好的堆，重复计算导致性能低下。

✅顺着不行只能“逆天而行”，自底向上、逐层建堆。从最后一个非叶子节点开始建堆，那它的左右孩子必为叶子节点，叶子节点相当于已经建好的堆。逐层往上，当你在父节点 i 上调用 siftDown 时，它的左右子树都已经是堆了（因为你先处理好更深层的节点）。这样，单次 siftDown 只需要把第 i 个节点“插入”到一个已经是堆的子树里，最终整棵树就成为堆。

相当于已经计算好的结果，可以应用到后面的计算，从而避免不必要的重复计算，大大提高建堆性能。

在线性时间内、一步到位地把数组“堆化”

4.2.2. 计算建堆时间复杂度

建堆总工作量分析计算：

在批量 heapify 中，只有非叶节点会执行下沉。完美二叉树上共有约 n/2 个非叶节点。

那么，可以下沉至少 1 层 的节点最多有多少呢？

最多是所有非叶节点都可以下沉1层，一共≤ n/2次单步下沉

可以下沉至少 2 层 的节点最多有多少？

只有距叶子深度 ≥2 的节点，一共 ≤n/4次单步下沉

可以下沉至少 3 层 的节点数最多有多少？

只有距叶子深度 ≥3 的节点，一共 ≤n/8次单步下沉

...

一直到堆顶，可能的最大下沉深度k层，一共 ≤n/2^k次单步下沉

总单步下沉数
把“下沉至少 k 层”的所有单步加起来，就是下沉总次数

时间复杂度计算

元素拷贝： 将整个数组元素直接拷贝到内部 queue 数组，时间复杂度O(n)；

最终总工作量=元素拷贝 + 建堆的时间复杂度=O(n) + O(n) = O(n)

批量建堆时间复杂度计算可视化：

批量建堆时间复杂度计算

对比入队和建堆的时间复杂度：

方法	时间复杂度	何时使用
入队＋siftUp	O(n log n)	动态地一个个插入元素
一次性 heapify＋siftDown	O(n)	已有一整个数组，一次建堆

💡 5. 应用实战

5.1. 小顶堆

默认就是小顶堆

PriorityQueue<String> priorityQueue = new PriorityQueue<>();
priorityQueue.offer("1");
priorityQueue.offer("5");
priorityQueue.offer("3");
priorityQueue.offer("7");
priorityQueue.offer("9");

System.out.println(priorityQueue);

priorityQueue.poll();

System.out.println(priorityQueue);

测试结果：

[1, 5, 3, 7, 9]
[3, 5, 9, 7]

5.2. 大顶堆

想实现最大堆？传入 Comparator 即可：

PriorityQueue<String> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
maxHeap.offer("1");
maxHeap.offer("5");
maxHeap.offer("3");
maxHeap.offer("7");
maxHeap.offer("9");
System.out.println(maxHeap);

maxHeap.poll();

System.out.println(maxHeap);

测试结果

[9, 7, 3, 1, 5]
[7, 5, 3, 1]

5.3. 比较器

堆内元素为自定义对象Person，实现 默认按年龄降序 排序（即年龄越大优先）

具体源码如下：

public class Person implements Comparable<Person>{
    private String name;
    private Integer age;

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public Integer getAge() {
        return age;
    }

    public void setAge(Integer age) {
        this.age = age;
    }

    public Person(String name, Integer age) {
        this.name = name;
        this.age = age;
    }
    @Override
    public int compareTo(Person other) {
//        return this.age.compareTo(other.age);  // 小顶堆：按年龄升序
        // 大顶堆：降序：年龄大的排前面
        return other.age.compareTo(this.age);
    }

    @Override
    public String toString() {
        return name + " (" + age + ")";
    }

    public static void main(String[] args) {
        PriorityQueue<Person> personPriorityQueue = new PriorityQueue<>();
        personPriorityQueue.offer(new Person("张三",28));
        personPriorityQueue.offer(new Person("李四",21));
        personPriorityQueue.offer(new Person("渊渟岳",18));
        personPriorityQueue.offer(new Person("咿呀呀",19));
        System.out.println(personPriorityQueue);
    }

}

执行结果：

[张三 (28), 李四 (21), 渊渟岳 (18), 咿呀呀 (19)]

同样可以对它做取反操作，变为小顶堆，从小到大的年龄排序

PriorityQueue<Person> personPriorityQueue = new PriorityQueue<>(Comparator.reverseOrder());
personPriorityQueue.offer(new Person("张三",28));
personPriorityQueue.offer(new Person("李四",21));
personPriorityQueue.offer(new Person("渊渟岳",18));
personPriorityQueue.offer(new Person("咿呀呀",19));
System.out.println(personPriorityQueue);

执行结果：

[渊渟岳 (18), 咿呀呀 (19), 李四 (21), 张三 (28)]

5.4. 找出年龄最大的前 K 个人

我们来实现一个典型的 Top-K 最大年龄的 Person 问题。

实现思路：

使用 PriorityQueue<Person>，保存堆顶为当前第 K 大的元素，大小为 K；

遍历所有元素：如果堆未满：加入；如果堆满，且当前元素年龄大于堆顶：替换堆顶；

最终堆中就是 Top-K 最大年龄的 Person。

具体源码如下：

public class TopKDemo {
    /**
     * 获取数组中 前 K 个最小或最大的元素
     *  这里实现的是 前 K 个年龄大的
     */
    public static List<Person> getTopKByAge(List<Person> people, int k) {
        if (people == null)
            throw new RuntimeException("家里没有人");
        // 小顶堆：堆顶是当前 Top-K 里最小年龄的，因为Person类是正序排序
        PriorityQueue<Person> minHeap = new PriorityQueue<>(k);

        for (Person p : people) {
            if (minHeap.size() < k) {
                minHeap.offer(p);
            }
            // 堆满 K 个元素后，取堆顶判断元素大小
            else if (p.compareTo(minHeap.peek())>0) {
                minHeap.poll();
                minHeap.offer(p);
            }
        }
        // 转换回 List
        List<Person> result = new ArrayList<>(minHeap);
        return result;
    }

    public static void main(String[] args) {
        // 测试数据
        List<Person> people = Arrays.asList(
                new Person("张三", 28),
                new Person("李四", 21),
                new Person("渊渟岳", 18),
                new Person("咿呀呀", 19),
                new Person("王五", 33),
                new Person("老六", 33)
        );

        int k = 3;
        List<Person> topK = getTopKByAge(people, k);
        System.out.println("Top " + k + " 最老的人:");
        topK.forEach(System.out::println);
    }
}

执行结果

Top 3 最老的人:
张三 (28)
王五 (33)
老六 (33)

这里容易搞错的点是：大顶堆和小顶堆的选择上。

取前K个最大元素，得选用小顶堆，这样才能确保每次比较大小时，都是和堆内最小的元素进行比较，取出最小的，留下最大的元素在堆内。

PriorityQueue 适用于：取数组前 K 个最小或最大的元素

5.5. 购买游戏装备问题

先定义一个购买装备的配置对象，用来保持配置优先级信息，规定priority 数字越小优先购买。

public class EquipmentItem implements Comparable<EquipmentItem> {
    private final String name;
    private final int priority; // 数字越小优先购买

    public EquipmentItem(String name, int priority) {
        this.name = name;
        this.priority = priority;
    }

    public String getName() {
        return name;
    }

    @Override
    public int compareTo(EquipmentItem other) {
        return Integer.compare(this.priority, other.priority);
    }

    @Override
    public String toString() {
        return String.format("%s (priority=%d)", name, priority);
    }
}

接着完成管理单个英雄的装备购买顺序

/**
 * 管理单个英雄的装备购买顺序
 */
public class HeroEquipmentPlan {
    private final String heroName;
    private final PriorityQueue<EquipmentItem> planQueue = new PriorityQueue<>();

    public HeroEquipmentPlan(String heroName) {
        this.heroName = heroName;
    }

    /**
     * 预先设置一系列装备及其优先级
     */
    public void addItem(String itemName, int priority) {
        planQueue.offer(new EquipmentItem(itemName, priority));
        System.out.println("添加装备到购买计划: " + itemName + "，优先级为：" + priority);
    }

    /**
     * 获取下一个最优先购买的装备
     */
    public EquipmentItem getNextItem() {
        EquipmentItem next = planQueue.poll();
        if (next == null) {
            System.out.println("全部购买完成：" + heroName);
        } else {
            System.out.println("下一个购买项：" + heroName + ": " + next);
        }
        return next;
    }

    /**
     * 查看当前购买计划（不移除）
     */
    public void previewPlan() {
        System.out.println("当前购买计划：" + heroName + ":");
        planQueue.stream()
                .sorted()
                .forEach(item -> System.out.println("  - " + item));
    }

}

测试装备购买顺序配置，再进行装备购买

public class Demo{
    public static void main(String[] args) {
        // 游戏开始前：为英雄设置购买优先级
        HeroEquipmentPlan plan = new HeroEquipmentPlan("战士");
        plan.addItem("长剑", 1);
        plan.addItem("护甲", 2);
        plan.addItem("靴子", 3);
        plan.addItem("暴击手套", 4);
        plan.addItem("巨人腰带", 5);

        // 开局预览
        plan.previewPlan();

        // 游戏中：当有足够金币时，依次购买下一个装备
        EquipmentItem next;
        while ((next = plan.getNextItem()) != null) {
            // 在这里调用游戏购买接口或提醒玩家：
            // buyItem(next.getName());
            // 模拟购买间隔
            try {
                Thread.sleep(2000);
            } catch (InterruptedException ignored) {}
        }

        System.out.println("购买计划已完成，祝游戏愉快！");
    }
}

测试结果:

添加装备到购买计划: 长剑，优先级为：1
添加装备到购买计划: 护甲，优先级为：2
添加装备到购买计划: 靴子，优先级为：3
添加装备到购买计划: 暴击手套，优先级为：4
添加装备到购买计划: 巨人腰带，优先级为：5
当前购买计划：战士:
  - 长剑 (priority=1)
  - 护甲 (priority=2)
  - 靴子 (priority=3)
  - 暴击手套 (priority=4)
  - 巨人腰带 (priority=5)
下一个购买项：战士: 长剑 (priority=1)
下一个购买项：战士: 护甲 (priority=2)
下一个购买项：战士: 靴子 (priority=3)
下一个购买项：战士: 暴击手套 (priority=4)
下一个购买项：战士: 巨人腰带 (priority=5)
全部购买完成：战士
购买计划已完成，祝游戏愉快！

PriorityQueue 适用于：管理优先级任务调度

📈 6. 汇总

6.1. 时间复杂度汇总

操作	时间复杂度
入队 offer()	O(log n)
出队 poll()	O(log n)
访问 peek()	O(1)
建堆 heapify	O(n)
循环入队式建堆	O(n log n)

6.2. 常见误区

误区	正解
`PriorityQueue` 是 FIFO？❌	✅ 它默认是最小堆，优先出最小元素
删除元素快？❌	✅ 仅堆顶是 O(log n)，任意删除是 O(n)
支持 null 元素？❌	✅ 不允许插入 null，会抛异常
是线程安全的吗？❌	✅ 需要手动加锁或使用线程安全版本`PriorityBlockingQueue`

📚 7. 总结

二叉堆就四句话：有批量选批量，没批量逐个建；获取最优数值，重建合法堆形。

PriorityQueue 优先队列和普通的二叉堆一样，主要分为三部分：初建堆、取最值、重建堆。其中建堆分为两种情况：逐个入队建堆和批量建堆。

PriorityQueue 是建立在小顶堆结构上的非线程安全队列，底层数据结构为数组，核心处理逻辑为二叉堆，通过 siftUp 和 siftDown 动态维护堆结构，默认最小堆，但可以通过 Comparator 灵活定制。

适合优先级任务调度、动态最值维护、Top-K等场景。注意线程安全与迭代顺序的问题，在并发场景下使用 PriorityBlockingQueue。

往期推荐

分类	往期文章
Java集合底层原理可视化	Java 集合--快速掌握涵盖三大场景实现的Set集合底层原理 ArrayDeque双端队列--底层原理可视化 “子弹弹夹”装弹和出弹的抽象原理实战：掌握栈的原理与实战 TreeMap集合--底层原理、源码阅读及它在Java集合框架中扮演什么角色？ LinkedHashMap集合--原理可视化 HashMap集合--基本操作流程的源码可视化 Java集合--HashMap底层原理可视化，秒懂扩容、链化、树化 Java集合--从本质出发理解HashMap Java集合--LinkedList源码可视化 Java集合源码--ArrayList的可视化操作过程
设计模式秘籍（已全部开源）	掌握设计模式的两个秘籍往期设计模式文章的：设计模式
软件设计师	软考中级--软件设计师毫无保留的备考分享软件设计师--案例分析题轻松上分，解决你的备考烦恼通过软考后却领取不到实体证书？ 2023年下半年软考考试重磅消息
Java学习路线和相应资源	Java全栈学习路线、学习资源和面试题一条龙

原创不易，觉得还不错的，三连支持：点赞、分享、推荐↓

文章来源:https://www.cnblogs.com/dennyLee2025/p/19067516
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！

标签：

上一篇：Java深拷贝与浅拷贝核心解析
下一篇：12K+ Star！新一代的开源持续测试工具！

首页 > 面试资料博客日记

PriorityQueue 数据结构底层原理、源码实现可视化分析及应用实战

🚀 1. 概述

1.1. PriorityQueue 是什么？

1.2. 底层数据结构

1.3. 二叉堆的规律

⚙️ 2. 入队相关操作

2.1. 入队操作

2.2. 扩容操作

🗑 3. 出队操作

🏗️ 4. 批量建堆（heapify）

4.1. heapify 源码逻辑

4.2. 为什么自底向上更快？

4.2.1. 为什么选择自底向上、逐层下沉？

4.2.2. 计算建堆时间复杂度

💡 5. 应用实战

5.1. 小顶堆

5.2. 大顶堆

5.3. 比较器

5.4. 找出年龄最大的前 K 个人

5.5. 购买游戏装备问题

📈 6. 汇总

6.1. 时间复杂度汇总

6.2. 常见误区

📚 7. 总结

往期推荐

相关文章

最新发布

点击排行

本站推荐

标签云

首页 > 面试资料 博客日记

PriorityQueue 数据结构底层原理、源码实现可视化分析及应用实战

🚀 1. 概述

1.1. PriorityQueue 是什么？

1.2. 底层数据结构

1.3. 二叉堆的规律

⚙️ 2. 入队相关操作

2.1. 入队操作

2.2. 扩容操作

🗑 3. 出队操作

🏗️ 4. 批量建堆（heapify）

4.1. heapify 源码逻辑

4.2. 为什么自底向上更快？

4.2.1. 为什么选择自底向上、逐层下沉？

4.2.2. 计算建堆时间复杂度

💡 5. 应用实战

5.1. 小顶堆

5.2. 大顶堆

5.3. 比较器

5.4. 找出年龄最大的前 K 个人

5.5. 购买游戏装备问题

📈 6. 汇总

6.1. 时间复杂度汇总

6.2. 常见误区

📚 7. 总结

往期推荐

相关文章

最新发布

点击排行

本站推荐

标签云

首页 > 面试资料博客日记