数据结构：阶段测试(查漏补缺)

这篇文章介绍了数据结构：阶段测试(查漏补缺)，分享给大家做个参考，收藏Java资料网收获更多编程知识

目录

选择题：

题一：

题二：

题三：

题四：

编程题：

题一：左叶子之和

思路一：

题二：约瑟夫问题（用单链表实现）

思路一：

本人实力有限可能对一些地方解释和理解的不够清晰，可以自己尝试读代码，或者评论区指出错误，望海涵！

感谢大佬们的一键三连！ 感谢大佬们的一键三连！ 感谢大佬们的一键三连！

---

选择题：

题一：

1.将长度为n的单链表连接在长度为m的单链表之后,其算法的时间复杂度为() 

A. O(m)

B. O(1)

C. O(n)

D. O(m+n)

答案解析：

        长度为n的单链表链接长度为m的单链表只需要长度为m的单链表的头节点的地址，所以时间复杂度还是O(n)。

题二：

2.以下属于链表的优点的是（ ）

A. 用数组可方便实现

B. 插入操作效率高

C. 不用为节点间的逻辑关系而增加额外的存储开销

D. 可以按元素号随机访问

答案解析：

        链表插入不需要挪动数据，所以插入效率高。

题三：

3.对于序列{ 12,13,11,18,60,15,7,19,25,100 }，用筛选法建堆，应该从值为（）的数据开始建初始堆

A. 100

B. 12

C. 60

D. 15

答案解析：

        一共有10个数据，下标为0--9，建堆需要从最后一层的父节点开始，所以,最后一个元素的父节点为：(9 - 1) / 2 = 4,以4为下标的元素为60.

题四：

4.将整数数组（ 7-6-3-5-4-1-2 ）按照堆排序的方式进行升序排列，请问在第一轮排序结束之后，数组的顺序是（）

A. 1-2-3-4-5-6-7

B. 2-6-3-5-4-1-7

C. 6-5-3-2-4-1-7

D. 5-4-3-2-1-6-7

答案解析：

        堆排序实现参考：数据结构：一篇拿捏十大排序(超详细版)-CSDN博客可知C正确。

编程题：

题一：左叶子之和

左叶子之和_牛客题霸_牛客网 (nowcoder.com)

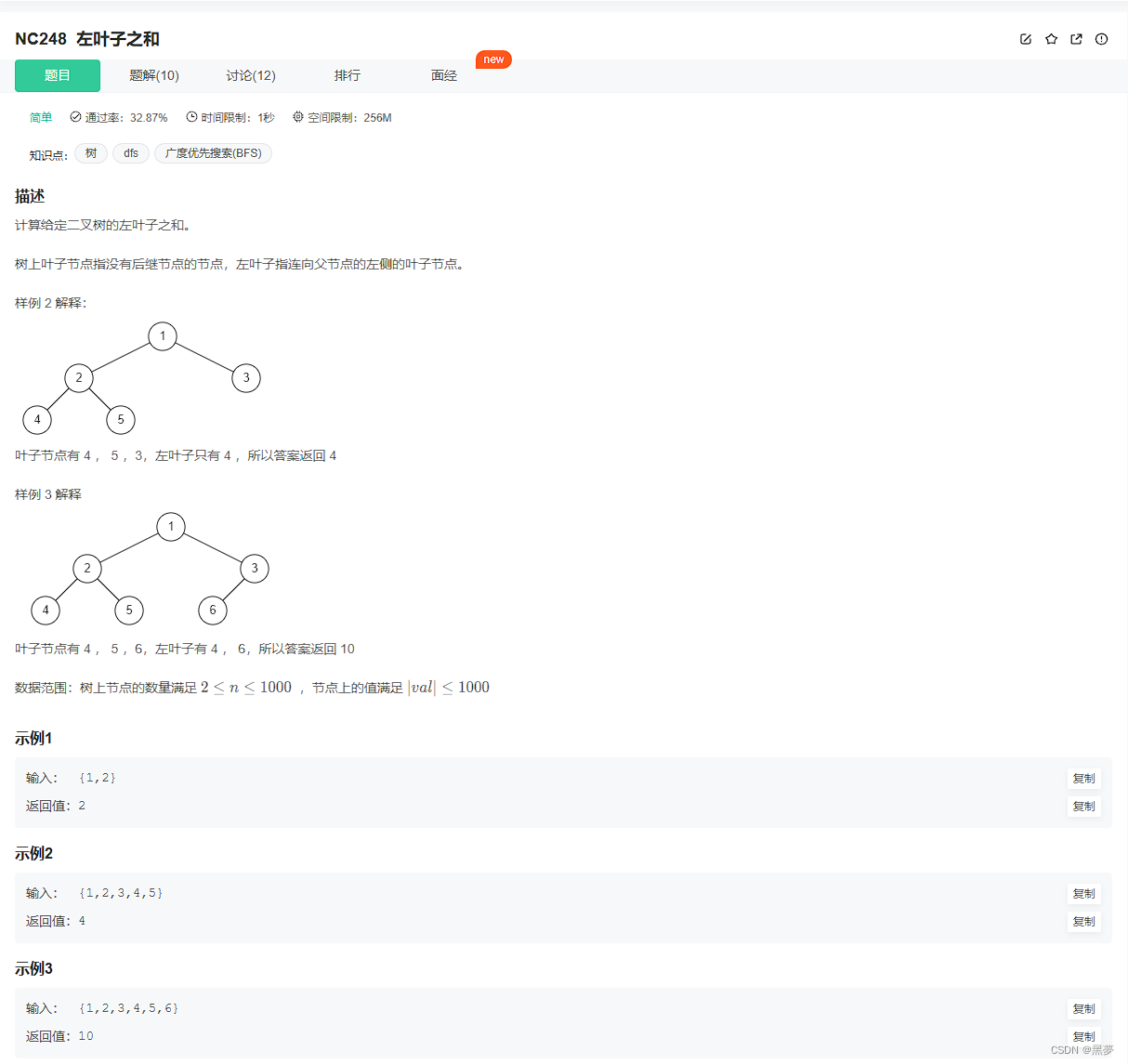
思路一：

        第一步：首先：判断是否为空树；

        第二步：在确保当前节点左子树存在的情况下，判断当前节点的左子树的左子树和右子树是否为空，为空则记录当前节点的左子树的值；

        第三步：将当前节点继续遍历左子树和右子树进行递归遍历整棵树，将所有符合第二步的节点值记录，最后合并，返回。

int sumOfLeftLeaves(struct TreeNode* root ) 
{
    if(root == NULL)
    {
        return 0;
    }
    int sum = 0;
    if(root->left && root->left->left == NULL && root->left->right == NULL)
    {
        sum +=  root->left->val;
    }

    sum += sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);

    return sum;
}

题二：约瑟夫问题（用单链表实现）

约瑟夫环__牛客网 (nowcoder.com)

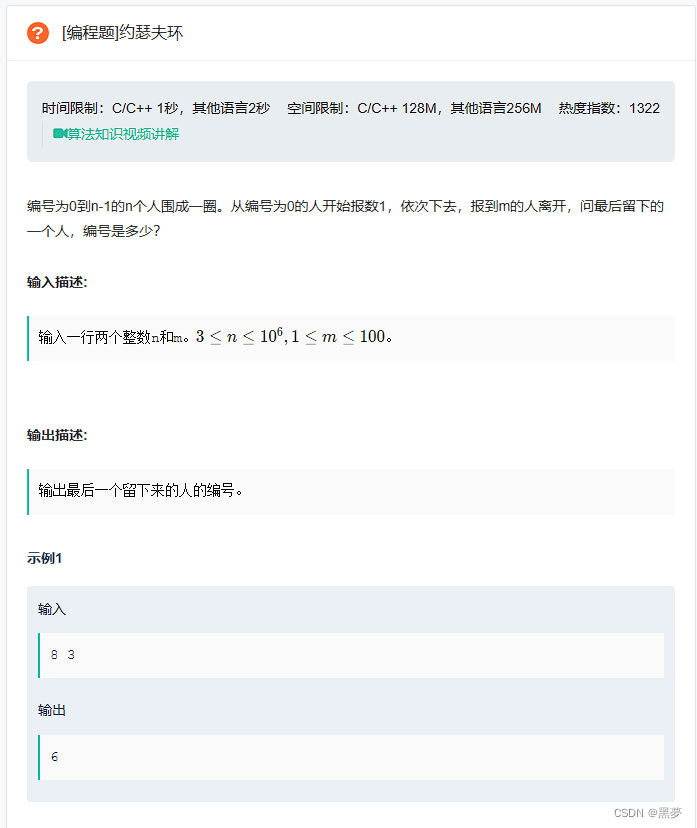
思路一：

        构建值为1~n的n个节点的循环链表2.实现约瑟夫环，借助cur从链表起始位置开始报数，因为约瑟夫环最终只剩余一个节点，即cur->next != cur时，说明链表中不止一个节点，则循环进行以下操作报数，即遍历链表，循环m-1次，循环停止时，cur即为报m的节点删除该节点，遍历时保存cur的前一个prev，删除cur，然后将cur放在prev的下一个;

        最后剩余的一个节点中的值域就是最后留下来的人。注意：在返回之后一定要把最后一个节点释放掉，否则会有内存泄漏。

#define _CRT_SECURE_NO_WARNINGS 1

//约瑟夫问题

#include <stdio.h>
typedef struct List
{
    struct List* front;
    int val;
    struct List* next;
}L;

L* Init(int x)
{
    L* tmp = (L*)malloc(sizeof(L));
    tmp->val = x;
    tmp->next = NULL;
    tmp->front = NULL;

    return tmp;
}

L* DeletNode(L* cur)
{
    L* old = cur->front;

    old->next = cur->next;
    old->next->front = old;
    L* new = old->next;

    free(cur);
    return new;
}

int main()
{
    L l;
    L* prve = Init(0);
    L* count = prve;
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        L* tmp = Init(i);
        tmp->front = prve;
        prve->next = tmp;
        prve = tmp;
    }

    prve->next = count->next;
    count->next->front = prve;
    L* cur = prve->next;
    free(count);

    while (cur->next != cur)
    {
        for (int j = 0; j < m - 1; j++)
        {
            cur = cur->next;
        }
        cur = DeletNode(cur);
    }
    printf("%d", cur->val);

    return 0;
}

本人实力有限可能对一些地方解释和理解的不够清晰，可以自己尝试读代码，或者评论区指出错误，望海涵！

感谢大佬们的一键三连！ 感谢大佬们的一键三连！ 感谢大佬们的一键三连！

                                              

文章来源:https://blog.csdn.net/weixin_71964780/article/details/134022470
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系邮箱：jacktools123@163.com进行投诉反馈，一经查实，立即删除！